Article contents
Local limit theorem for a Markov additive process on 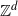 $\mathbb{Z}^d$ with a null recurrent internal Markov chain
$\mathbb{Z}^d$ with a null recurrent internal Markov chain
Published online by Cambridge University Press: 22 December 2022
Abstract
In the classical framework, a random walk on a group is a Markov chain with independent and identically distributed increments. In some sense, random walks are time and space homogeneous. This paper is devoted to a class of inhomogeneous random walks on 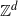 $\mathbb{Z}^d$ termed ‘Markov additive processes’ (also known as Markov random walks, random walks with internal degrees of freedom, or semi-Markov processes). In this model, the increments of the walk are still independent but their distributions are dictated by a Markov chain, termed the internal Markov chain. While this model is largely studied in the literature, most of the results involve internal Markov chains whose operator is quasi-compact. This paper extends two results for more general internal operators: a local limit theorem and a sufficient criterion for their transience. These results are thereafter applied to a new family of models of drifted random walks on the lattice
$\mathbb{Z}^d$ termed ‘Markov additive processes’ (also known as Markov random walks, random walks with internal degrees of freedom, or semi-Markov processes). In this model, the increments of the walk are still independent but their distributions are dictated by a Markov chain, termed the internal Markov chain. While this model is largely studied in the literature, most of the results involve internal Markov chains whose operator is quasi-compact. This paper extends two results for more general internal operators: a local limit theorem and a sufficient criterion for their transience. These results are thereafter applied to a new family of models of drifted random walks on the lattice  $\mathbb{Z}^d$.
$\mathbb{Z}^d$.
Keywords
Information
- Type
- Original Article
- Information
- Copyright
- © The Author(s), 2022. Published by Cambridge University Press on behalf of Applied Probability Trust
References
- 1
- Cited by


