Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Howard, C. Douglas
2004.
Probability on Discrete Structures.
Vol. 110,
Issue. ,
p.
125.
Kartun-Giles, Alexander P.
Barthelemy, Marc
and
Dettmann, Carl P.
2019.
Shape of shortest paths in random spatial networks.
Physical Review E,
Vol. 100,
Issue. 3,

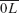 . Here, for Euclidean models in dimension
. Here, for Euclidean models in dimension 