Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Glendinning, R.H.
1991.
The convex hull of a dependent vector-valued process.
Journal of Statistical Computation and Simulation,
Vol. 38,
Issue. 1-4,
p.
219.
Guttorp, Peter
and
Thorarinsdottir, Thordis L.
2012.
What Happened to Discrete Chaos, the Quenouille Process, and the Sharp Markov Property? Some History of Stochastic Point Processes.
International Statistical Review,
Vol. 80,
Issue. 2,
p.
253.
Jupp, P.E.
2015.
Copulae on products of compact Riemannian manifolds.
Journal of Multivariate Analysis,
Vol. 140,
Issue. ,
p.
92.
Jones, M. C.
Pewsey, Arthur
and
Kato, Shogo
2015.
On a class of circulas: copulas for circular distributions.
Annals of the Institute of Statistical Mathematics,
Vol. 67,
Issue. 5,
p.
843.

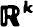 using a Markov sequence of points. Essentially, in the process
using a Markov sequence of points. Essentially, in the process 