Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Klebaner, Fima C.
1988.
Conditions for fixation of an allele in the density-dependent wright–Fisher models.
Journal of Applied Probability,
Vol. 25,
Issue. 02,
p.
247.
Grey, D. R.
1989.
A note on explosiveness of Markov branching processes.
Advances in Applied Probability,
Vol. 21,
Issue. 1,
p.
226.
Grey, D. R.
1989.
A note on explosiveness of Markov branching processes.
Advances in Applied Probability,
Vol. 21,
Issue. 01,
p.
226.
Chen, A. Y.
and
Renshaw, E.
1990.
Markov branching processes with instantaneous immigration.
Probability Theory and Related Fields,
Vol. 87,
Issue. 2,
p.
209.
Pakes, Anthony G.
1993.
Explosive Markov branching processes: entrance laws and limiting behaviour.
Advances in Applied Probability,
Vol. 25,
Issue. 04,
p.
737.
Vatutin, V. A.
and
Zubkov, A. M.
1993.
Branching processes. II.
Journal of Soviet Mathematics,
Vol. 67,
Issue. 6,
p.
3407.
Pakes, Anthony G.
2007.
Extinction and explosion of nonlinear Markov branching processes.
Journal of the Australian Mathematical Society,
Vol. 82,
Issue. 3,
p.
403.
Amini, Omid
Devroye, Luc
Griffiths, Simon
and
Olver, Neil
2013.
On explosions in heavy-tailed branching random walks.
The Annals of Probability,
Vol. 41,
Issue. 3B,
Chaumont, Loïc
and
Kyprianou, Andreas E.
2021.
A Lifetime of Excursions Through Random Walks and Lévy Processes.
Vol. 78,
Issue. ,
p.
1.
Foucart, Clément
and
Zhou, Xiaowen
2022.
On the explosion of the number of fragments in simple exchangeable fragmentation-coagulation processes.
Annales de l'Institut Henri Poincaré, Probabilités et Statistiques,
Vol. 58,
Issue. 2,
Vidmar, Matija
2022.
Some harmonic functions for killed Markov branching processes with immigration and culling.
Stochastics,
Vol. 94,
Issue. 4,
p.
578.
Foucart, Clément
and
Zhou, Xiaowen
2023.
On the boundary classification of Λ-Wright–Fisher processes with frequency-dependent selection.
Annales Henri Lebesgue,
Vol. 6,
Issue. ,
p.
493.

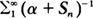 , where α ≧ 0 and
, where α ≧ 0 and 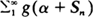 for a large class of functions
for a large class of functions 