Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Pham-Gia, T.
and
Turkkan, N.
2003.
Standby System Availability Using Gamma Approximation.
American Journal of Mathematical and Management Sciences,
Vol. 23,
Issue. 3-4,
p.
239.
Morozov, Evsey
2004.
Weak Regeneration in Modeling of Queueing Processes.
Queueing Systems,
Vol. 46,
Issue. 3-4,
p.
295.
Vlasiou, Maria
2011.
Wiley Encyclopedia of Operations Research and Management Science.
Morozov, E.
and
Steyaert, B.
2013.
Stability analysis of a two-station cascade queueing network.
Annals of Operations Research,
Vol. 202,
Issue. 1,
p.
135.
Morozov, Evsey
and
Steyaert, Bart
2021.
Stability Analysis of Regenerative Queueing Models.
p.
15.
Morozov, Evsey
and
Steyaert, Bart
2021.
Queueing Theory 2.
p.
239.
Morozov, Evsey
and
Rykov, Vladimir
2023.
On the Positive Recurrence of Finite Regenerative Stochastic Models.
Mathematics,
Vol. 11,
Issue. 23,
p.
4754.
Glynn, Peter
and
Qu, Yanlin
2023.
On a New Characterization of Harris Recurrence for Markov Chains and Processes.
Mathematics,
Vol. 11,
Issue. 9,
p.
2165.

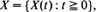 , the existence of a first regeneration time,
, the existence of a first regeneration time, 