Published online by Cambridge University Press: 14 July 2016
In this note we adopt the notation and terminology of Kingman (1966) without further comment. For the general single server queue one has
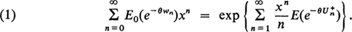 For the queueing system GI/Ek/1 it is possible to make use of the particular nature of the service time distribution to evaluate the right-hand side of Equation (1) in terms of the k roots of a certain equation. This evaluation is carried out in detail in Prabhu (1965) to which reference should be made for the technicalities involved. A similar evaluation applies to the limiting distribution
For the queueing system GI/Ek/1 it is possible to make use of the particular nature of the service time distribution to evaluate the right-hand side of Equation (1) in terms of the k roots of a certain equation. This evaluation is carried out in detail in Prabhu (1965) to which reference should be made for the technicalities involved. A similar evaluation applies to the limiting distribution
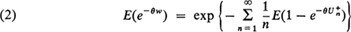 when it exists. However, the resulting expression again involves the k roots of a certain equation. In this note we draw attention to an alternative procedure which does not involve the calculation of roots. We remark that a similar, but slightly different, procedure can be used in the study of the queueing system Ek/GI/1. Details of this will be presented in a separate note.
when it exists. However, the resulting expression again involves the k roots of a certain equation. In this note we draw attention to an alternative procedure which does not involve the calculation of roots. We remark that a similar, but slightly different, procedure can be used in the study of the queueing system Ek/GI/1. Details of this will be presented in a separate note.