Article contents
On interpoint distances for planar Poisson cluster processes
Published online by Cambridge University Press: 14 July 2016
Abstract
For stationary Poisson or Poisson cluster processes ξ on R2 we study the distribution of the interpoint distances using the interpoint distance function 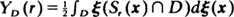 and the nearest-neighbor indicator function
and the nearest-neighbor indicator function 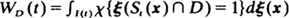 . Here Sr (x) is the interior of a circle of radius r having center x, I(t) is that subset of D which has x ∊ D and St (x) ⊂ D and χ is the usual indicator function. We show that if the region D ⊂ R2 is large, then these functions are approximately distributed as Poisson processes indexed by
. Here Sr (x) is the interior of a circle of radius r having center x, I(t) is that subset of D which has x ∊ D and St (x) ⊂ D and χ is the usual indicator function. We show that if the region D ⊂ R2 is large, then these functions are approximately distributed as Poisson processes indexed by 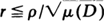 and
and 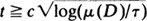 , where µ(D) is the Lebesgue measure of D.
, where µ(D) is the Lebesgue measure of D.
Information
- Type
- Research Papers
- Information
- Copyright
- Copyright © Applied Probability Trust 1983
Footnotes
Work supported by the National Science Foundation (MCS-79–03781) while both authors were employed by the Department of Mathematical Sciences, Northern Illinois University, DeKalb, IL 60115.
References
- 7
- Cited by

