Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Szabó, Gábor
Alava, Mikko
and
Kertész, János
2002.
Shortest paths and load scaling in scale-free trees.
Physical Review E,
Vol. 66,
Issue. 2,
Goh, William
and
Schmutz, Eric
2002.
Limit distribution for the maximum degree of a random recursive tree.
Journal of Computational and Applied Mathematics,
Vol. 142,
Issue. 1,
p.
61.
Chan, Derek Y. C.
Hughes, Barry D.
Leong, Alex S.
and
Reed, William J.
2003.
Stochastically evolving networks.
Physical Review E,
Vol. 68,
Issue. 6,
Panholzer, Alois
2004.
The distribution of the size of the ancestor‐tree and of the induced spanning subtree for random trees.
Random Structures & Algorithms,
Vol. 25,
Issue. 2,
p.
179.
Bollobás, Béla
and
Riordan, Oliver
2004.
Shortest paths and load scaling in scale-free trees.
Physical Review E,
Vol. 69,
Issue. 3,
Panholzer, Alois
and
Prodinger, Helmut
2004.
Spanning tree size in random binary search trees.
The Annals of Applied Probability,
Vol. 14,
Issue. 2,
Su, Chun
Liu, Jie
and
Feng, Qunqiang
2006.
A note on the distance in random recursive trees.
Statistics & Probability Letters,
Vol. 76,
Issue. 16,
p.
1748.
Feng, Qunqiang
and
Su, Chun
2007.
The structure and distances in Yule recursive trees.
Random Structures & Algorithms,
Vol. 31,
Issue. 3,
p.
273.
Dorogovtsev, S. N.
Krapivsky, P. L.
and
Mendes, J. F. F.
2008.
Transition from small to large world in growing networks.
EPL (Europhysics Letters),
Vol. 81,
Issue. 3,
p.
30004.
Dorogovtsev, Sergey N.
2009.
Encyclopedia of Complexity and Systems Science.
p.
4486.
Kuba, Markus
and
Panholzer, Alois
2010.
On the distribution of distances between specified nodes in increasing trees.
Discrete Applied Mathematics,
Vol. 158,
Issue. 5,
p.
489.
Dorogovtsev, Sergey N.
2012.
Computational Complexity.
p.
1488.
Devroye, Luc
Fawzi, Omar
and
Fraiman, Nicolas
2012.
Depth Properties of scaled attachment random recursive trees.
Random Structures & Algorithms,
Vol. 41,
Issue. 1,
p.
66.
Fuchs, Michael
and
Lee, Chung-Kuei
2015.
The Wiener Index of Random Digital Trees.
SIAM Journal on Discrete Mathematics,
Vol. 29,
Issue. 1,
p.
586.
Dorogovtsev, Sergey N.
2015.
Encyclopedia of Complexity and Systems Science.
p.
1.
Wohl, Shirlee
Giles, John R.
Lessler, Justin
and
Pitzer, Virginia E.
2021.
Sample size calculation for phylogenetic case linkage.
PLOS Computational Biology,
Vol. 17,
Issue. 7,
p.
e1009182.
Lodewijks, Bas
2022.
On joint properties of vertices with a given degree or label in the random recursive tree.
Electronic Journal of Probability,
Vol. 27,
Issue. none,
Boci, Erion-Stelios
and
Mailler, Cécile
2023.
Large deviation principle for a stochastic process with random reinforced relocations.
Journal of Statistical Mechanics: Theory and Experiment,
Vol. 2023,
Issue. 8,
p.
083206.
Desmarais, Colin
2024.
Depths in random recursive metric spaces.
Journal of Applied Probability,
Vol. 61,
Issue. 4,
p.
1448.
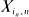 is asymptotically normal in several settings.
is asymptotically normal in several settings.
