Hostname: page-component-686fd747b7-8s9h2 Total loading time: 0 Render date: 2025-02-13T11:31:38.417Z Has data issue: false hasContentIssue false
  • English
  • Français

Perron–Frobenius theory for kernels and Crump–Mode–Jagers processes with macro-individuals

Part of: Markov processes

Published online by Cambridge University Press:  04 September 2020

Serik Sagitov Open the ORCID record for Serik Sagitov [Opens in a new window]
Serik Sagitov*
Affiliation:
Chalmers University of Technology and University of Gothenburg
*
*Postal address: Chalmers University of Technology, SE-412 96 Gothenburg, Sweden. Email: serik@chalmers.se
Get access Rights & Permissions [Opens in a new window]

Abstract

Perron–Frobenius theory developed for irreducible non-negative kernels deals with so-called R-positive recurrent kernels. If the kernel M is R-positive recurrent, then the main result determines the limit of the scaled kernel iterations 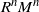$R^nM^n$ as $n\to\infty$ . In Nummelin (1984) this important result is proven using a regeneration method whose major focus is on M having an atom. In the special case when 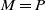$M=P$ is a stochastic kernel with an atom, the regeneration method has an elegant explanation in terms of an associated split chain. In this paper we give a new probabilistic interpretation of the general regeneration method in terms of multi-type Galton–Watson processes producing clusters of particles. Treating clusters as macro-individuals, we arrive at a single-type Crump–Mode–Jagers process with a naturally embedded renewal structure.

Keywords

Irreducible non-negative kernelsmulti-type Galton–Watson processpositive recurrent kernel

MSC classification

Primary: 60J05: Discrete-time Markov processes on general state spaces
Secondary: 60J80: Branching processes (Galton-Watson, birth-and-death, etc.)
Type
Research Papers
Information
Journal of Applied Probability , Volume 57 , Issue 3 , September 2020 , pp. 720 - 733
Check for updates
Copyright
© Applied Probability Trust 2020

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Athreya, K. andNey, P. (1972) Branching Processes. John Wiley, New York.Google Scholar
Athreya, K. andNey, P. (1982) A renewal approach to the Perron–Frobenius theory of non-negative kernels on general state spaces. Math. Z. 179, 507–530.CrossRefGoogle Scholar
Feller, W. (1959). An Introduction to Probability Theory and its Applications, Vol I, 2nd edn. John Wiley, New York.Google Scholar
Harris, T. E. (1963) The Theory of Branching Processes. Springer, Berlin.10.1007/978-3-642-51866-9CrossRefGoogle Scholar
Jagers, P. (1975) Branching Processes with Biological Applications. John Wiley, New York.Google Scholar
Jagers, P. andSagitov, S. (2008) General branching processes in discrete time as random trees. Bernoulli 14, 949–962.CrossRefGoogle Scholar
Lindo, A. andSagitov, S. (2018) General linear-fractional branching processes with discrete time. Stochastics 90, 364–378.10.1080/17442508.2017.1357722CrossRefGoogle Scholar
Mode, C. J. (1971) Multitype Branching Processes: Theory and Applications (Modern Analytic and Computational Methods in Science And Mathematics 34). Elsevier, New York.Google Scholar
Nummelin, E. (1984) General Irreducible Markov Chains and Non-negative Operators. Cambridge University Press.10.1017/CBO9780511526237CrossRefGoogle Scholar
Olofsson, P. (1996) Branching processes with local dependencies. Ann. Appl. Prob. 6, 238–268.Google Scholar
Sagitov, S. (2013) Linear-fractional branching processes with countably many types. Stoch. Process. Appl. 123, 2940–2956.10.1016/j.spa.2013.03.008CrossRefGoogle Scholar