Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Klebaner, F. C.
1984.
Geometric rate of growth in population-size-dependent branching processes.
Journal of Applied Probability,
Vol. 21,
Issue. 01,
p.
40.
Klebaner, F. C.
1984.
On population-size-dependent branching processes.
Advances in Applied Probability,
Vol. 16,
Issue. 1,
p.
30.
Klebaner, F. C.
1984.
On population-size-dependent branching processes.
Advances in Applied Probability,
Vol. 16,
Issue. 1,
p.
30.
Klebaner, F. C.
1985.
A limit theorem for population-size-dependent branching processes.
Journal of Applied Probability,
Vol. 22,
Issue. 01,
p.
48.
Höpfner, R.
1985.
A note on the probability of extinction in a class of population-size-dependent Galton-Watson processes.
Journal of Applied Probability,
Vol. 22,
Issue. 04,
p.
920.
Höpfner, Reinhard
1985.
On some classes of population-size-dependent Galton–Watson processes.
Journal of Applied Probability,
Vol. 22,
Issue. 01,
p.
25.
Höpfner, Reinhard
1986.
Some results on population-size-dependent Galton-Watson processes.
Journal of Applied Probability,
Vol. 23,
Issue. 02,
p.
297.
Loeffler, Markus
and
Grossmann, Bernd
1991.
A stochastic branching model with formation of subunits applied to the growth of intestinal crypts.
Journal of Theoretical Biology,
Vol. 150,
Issue. 2,
p.
175.
Parthasarathy, P.R.
and
Kumar, B.Krishna
1991.
Density-dependent birth and death process with state-dependent immigration.
Mathematical and Computer Modelling,
Vol. 15,
Issue. 1,
p.
11.
Parthasarathy, P. R.
and
Kumar, B. Krishna
1993.
Density‐dependent birth and death processes with immigration.
International Journal of Mathematical Education in Science and Technology,
Vol. 24,
Issue. 1,
p.
55.
Vatutin, V. A.
and
Zubkov, A. M.
1993.
Branching processes. II.
Journal of Soviet Mathematics,
Vol. 67,
Issue. 6,
p.
3407.
Klebaner, F. C.
1997.
Classical and Modern Branching Processes.
Vol. 84,
Issue. ,
p.
165.
Wang, Hanxing
and
Dai, Yonglong
1998.
Population-size-dependent branching processes in Markovian random environments.
Chinese Science Bulletin,
Vol. 43,
Issue. 8,
p.
635.
Li, Yuqiang
2006.
On a Continuous-State Population-Size-Dependent Branching Process and Its Extinction.
Journal of Applied Probability,
Vol. 43,
Issue. 01,
p.
195.
Jacob, Christine
2008.
Mathematical Modeling of Biological Systems, Volume II.
p.
339.
2010.
Introduction to Stochastic Models.
p.
343.
Jacob, Christine
2010.
Branching Processes: Their Role in Epidemiology.
International Journal of Environmental Research and Public Health,
Vol. 7,
Issue. 3,
p.
1186.

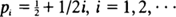 , depends on the population size, 2
, depends on the population size, 2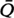 of positive probability.
of positive probability. 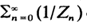 diverges almost surely on
diverges almost surely on 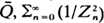 converges almost surely on
converges almost surely on  and there are no constants
and there are no constants 