Hostname: page-component-78c5997874-ndw9j Total loading time: 0 Render date: 2024-11-10T15:32:12.721Z Has data issue: false hasContentIssue false
  • English
  • Français

Random splittings of an interval

Part of: Special processes Limit theorems

Published online by Cambridge University Press:  14 July 2016

T. S. Mountford  and
S. C. Port
T. S. Mountford*
Affiliation:
University of California, Los Angeles
S. C. Port*
Affiliation:
University of California, Los Angeles
*
∗ Postal address: Department of Mathematics, University of California Los Angeles, CA 90024-1555, USA.
∗ Postal address: Department of Mathematics, University of California Los Angeles, CA 90024-1555, USA.
Get access Rights & Permissions [Opens in a new window]

Abstract

Points are independently and uniformly distributed onto the unit interval. The first n—1 points subdivide the interval into n subintervals. For 1 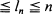we find a necessary and sufficient condition on {ln} for the events [Xn belongs to the ln th largest subinterval] to occur infinitely often or finitely often with probability 1. We also determine when the weak and strong laws of large numbers hold for the length of the ln th largest subinterval. The strong law of large numbers and the central limit theorem are shown to be valid for the number of times by time n the events [Xr belongs to lr th largest subinterval] occur when these events occur infinitely often.

Keywords

SPACINGSORDER STATISTICSUNIFORM DISTRIBUTION

MSC classification

Primary: 60K99: None of the above, but in this section
Secondary: 60F05: Central limit and other weak theorems 60F15: Strong theorems
Type
Research Papers
Information
Journal of Applied Probability , Volume 30 , Issue 1 , March 1993 , pp. 131 - 152
Copyright
Copyright © Applied Probability Trust 1993 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

Research partially supported by NSF Grant DMS86-01800 and DMS 91-57461.

References

[1] Bruss, F. T., Jammalamadaka, S. R. and Zhou, X. (1990) On an interval splitting problem. Statist. Prob. Lett. 10, 321–324.CrossRefGoogle Scholar
[2] Deheuvels, P. (1981) The strong approximation of extremal processes. Z. Wahrscheinlichkeitsth. 58, 1–6.CrossRefGoogle Scholar
[3] Deheuvels, P. (1982) Strong limiting bounds for maximal uniform spacings. Ann. Prob. 10, 1058–1065.CrossRefGoogle Scholar
[4] Deheuvels, P. (1983) Upper bounds for kth maximal spacings. Z. Wahrscheinlichkeitsth. 62, 465–474.CrossRefGoogle Scholar
[5] Devroye, L. (1981) Laws of the iterated logarithm for order statistics of uniform spacings. Ann. Prob. 9, 860–867.CrossRefGoogle Scholar
[6] Devroye, L. (1982) A log law for maximal uniform spacings. Ann. Prob. 10, 863–868.CrossRefGoogle Scholar
[7] Hall, P. and Heyde, C. C. (1980) Martingale Limit Theory and its Applications. Academic Press, New York.Google Scholar
[8] Holst, L. (1980) On the lengths of the pieces of a stick broken at random. J. Appl. Prob. 17, 623–634.CrossRefGoogle Scholar
[9] Pyke, R. (1965) Spacings. J. R. Statist. Soc. B27, 395–449.Google Scholar
[10] Pyke, R. (1972) Spacings revisited. Proc. 6th Berkeley Symp. Math. Statist. Prob. 1, 417–427.Google Scholar