Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
1998.
Records.
p.
279.
Doukhan, Paul
Klesov, Oleg I.
Pakes, Anthony G.
and
Steinebach, Josef G.
2013.
Limit theorems for record counts and times in the F α -scheme.
Extremes,
Vol. 16,
Issue. 2,
p.
147.
Doukhan, Paul
Klesov, Oleg I.
and
Steinebach, Josef G.
2015.
Mathematical Statistics and Limit Theorems.
p.
287.

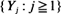 are analyzed, where {
are analyzed, where {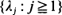 , a wide spectrum of behaviour is exhibited.
, a wide spectrum of behaviour is exhibited.