Article contents
R-positivity and the existence of zero-temperature limits of Gibbs measures on nearest-neighbor matrices
Published online by Cambridge University Press: 25 September 2023
Abstract
We study the 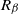 $R_\beta$-positivity and the existence of zero-temperature limits for a sequence of infinite-volume Gibbs measures
$R_\beta$-positivity and the existence of zero-temperature limits for a sequence of infinite-volume Gibbs measures 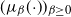 $(\mu_{\beta}(\!\cdot\!))_{\beta \geq 0}$ at inverse temperature
$(\mu_{\beta}(\!\cdot\!))_{\beta \geq 0}$ at inverse temperature 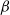 $\beta$ associated to a family of nearest-neighbor matrices
$\beta$ associated to a family of nearest-neighbor matrices 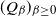 $(Q_{\beta})_{\beta \geq 0}$ reflected at the origin. We use a probabilistic approach based on the continued fraction theory previously introduced in Ferrari and Martínez (1993) and sharpened in Littin and Martínez (2010). Some necessary and sufficient conditions are provided to ensure (i) the existence of a unique infinite-volume Gibbs measure for large but finite values of
$(Q_{\beta})_{\beta \geq 0}$ reflected at the origin. We use a probabilistic approach based on the continued fraction theory previously introduced in Ferrari and Martínez (1993) and sharpened in Littin and Martínez (2010). Some necessary and sufficient conditions are provided to ensure (i) the existence of a unique infinite-volume Gibbs measure for large but finite values of 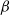 $\beta$, and (ii) the existence of weak limits as
$\beta$, and (ii) the existence of weak limits as 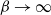 $\beta \to \infty$. Some application examples are revised to put in context the main results of this work.
$\beta \to \infty$. Some application examples are revised to put in context the main results of this work.
Information
- Type
- Original Article
- Information
- Copyright
- © The Author(s), 2023. Published by Cambridge University Press on behalf of Applied Probability Trust
References
A correction has been issued for this article:
- 1
- Cited by
Linked content
Please note a has been issued for this article.


