Hostname: page-component-78c5997874-j824f Total loading time: 0 Render date: 2024-11-10T15:20:20.998Z Has data issue: false hasContentIssue false
  • English
  • Français

Shock processes by aftereffects and multivariate lack of memory

Published online by Cambridge University Press:  14 July 2016

S. G. Ghurye  and
Albert W. Marshall
S. G. Ghurye*
Affiliation:
University of Alberta
Albert W. Marshall*
Affiliation:
University of British Columbia
*
∗Postal address: Department of Statistics and Applied Probability, The University of Alberta, Edmonton, Canada T6G 2G1.
∗∗Postal address: Department of Statistics, The University of British Columbia, #121-1984 Mathematics Road, Vancouver, BC, Canada V6T 1W5.
Get access Rights & Permissions [Opens in a new window]

Abstract

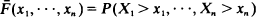If the survival function satisfies the functional equation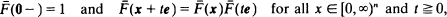

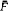where e = (1, …, 1), and if the marginal distributions are exponential, then is the multivariate exponential distribution of Marshall and Olkin. The functional equation has many solutions if the requirement of exponential marginals is not imposed, but the class of possible marginals is somewhat limited (e.g., marginals must be absolutely continuous). The class of possible solutions of the equation is characterized in this paper, and several examples are obtained from models for dependence that may be of practical interest.

Keywords

FATAL SHOCKSRELIABILITYSURVIVAL FUNCTION
Type
Research Papers
Information
Journal of Applied Probability , Volume 21 , Issue 4 , December 1984 , pp. 786 - 801
Copyright
Copyright © Applied Probability Trust 1984 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

Research sponsored in part by the Natural Sciences and Engineering Research Council of Canada.

Research sponsored in part by the Natural Sciences and Engineering Research Council of Canada and in part by the National Science Foundation at Stanford University.

This paper is dedicated to Dr Z. W. Birnbaum on the occasion of his 80th birthday.

References

Block, H. W. (1977) A characterization of a bivariate exponential distribution. Ann. Statist. 5, 808–812.Google Scholar
Block, H. W. and Basu, A. P. (1974) A continuous bivariate exponential extension. J. Amer. Statist. Assoc. 69, 1031–1037.Google Scholar
Esary, J. D., Proschan, F. and Walkup, D. W. (1967) Association of random variables, with application. Ann. Math. Statist. 38, 1466–1474.CrossRefGoogle Scholar
Ferman, P. (1981) A characterization of the multivariate exponential distribution. Vestnik Moskov. Univ. Ser. I, No. 4, 44–46.Google Scholar
Freund, J. E. (1961) A bivariate extension of the exponential distribution. J. Amer. Statist. Assoc. 56, 971–977.Google Scholar
Marshall, A. W. and Olkin, I. (1967) A multivariate exponential distribution. J. Amer. Statist. Assoc. 62, 30–44.Google Scholar