Hostname: page-component-78c5997874-4rdpn Total loading time: 0 Render date: 2024-11-10T17:28:15.839Z Has data issue: false hasContentIssue false
  • English
  • Français

Some characterizations of the Poisson process and geometric renewal process

Part of: Stochastic processes Distribution theory

Published online by Cambridge University Press:  14 July 2016

Wen-Jang Huang ,
Shun-Hwa Li  and
Jyh-Cherng Su
Shun-Hwa Li*
Affiliation:
National Sun Yat-sen University
*
Postal address for all authors: Institute of Applied Mathematics, National Sun Yat-sen University, Kaohsiung, Taiwan 80424, R.O.C.
Get access Rights & Permissions [Opens in a new window]

Abstract

Let γ t and δ t denote the residual life at t and current life at t, respectively, of a renewal process 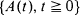, with 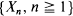the sequence of interarrival times. We prove that, given a function G, under mild conditions, as long as 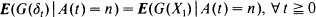holds for a single positive integer n, then 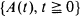is a Poisson process. On the other hand, for a delayed renewal process 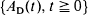with 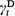the residual life at t, we find that for some fixed positive integer n, if 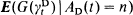is independent of t, then 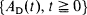is an arbitrarily delayed Poisson process. We also give some corresponding results about characterizing the common distribution function F of the interarrival times to be geometric when F is discrete. Finally, we obtain some characterization results based on the total life or independence of γ t and δ t.

Keywords

EXPONENTIAL DISTRIBUTIONGEOMETRIC DISTRIBUTIONMIXED RENEWAL PROCESS

MSC classification

Primary: 62E10: Characterization and structure theory
Secondary: 60G55: Point processes
Type
Research Papers
Information
Journal of Applied Probability , Volume 30 , Issue 1 , March 1993 , pp. 121 - 130
Copyright
Copyright © Applied Probability Trust 1993 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

∗

Support for this research was provided in part by the National Science Council of the Republic of China, Grant No. NSC 80–0208-MI 10–06.

References

Chung, K. L. (1972) The Poisson process as a renewal process. Period. Math. Hung. 2, 41–48.CrossRefGoogle Scholar
Çinlar, E. and Jagers, P. (1973) Two mean values which characterize the Poisson process. J. Appl. Prob. 10, 678–681.CrossRefGoogle Scholar
Erickson, B. K. and Guess, M. (1973) A characterization of the exponential law. Ann. Prob. 1, 183–185.CrossRefGoogle Scholar
Feigin, P. D. (1979) On the characterization of point process with the order statistic property. J. Appl. Prob. 16, 297–305.Google Scholar
Galambos, J. and Kotz, S. (1978) Characterizations of probability distribution. Lecture notes in Mathematics 675. Springer-Verlag, Berlin.Google Scholar
Gupta, P. L. and Gupta, R. C. (1986) A characterization of the Poisson process. J. Appl. Prob. 23, 233–235.Google Scholar
Holmes, P. T. (1974) Another characterization of the Poisson process. Sankhya A36, 449–450.Google Scholar
Huang, W. J., Li, S. H. and Su, J. C. (1991) Some characterizations of the Poisson process and geometric renewal process. Institute of Appl. Math., National Sun Yat-sen Univ., Tech. Report.Google Scholar
Karlin, S. and Taylor, H. M. (1975) A First Course in Stochastic Processes, 2nd edn. Academic Press, New York.Google Scholar
Lau, K. S. and Rao, B. L. C. P. (1990) Characterization of the exponential distribution by the relevation transform. J. Appl. Prob. 27, 726–729.Google Scholar
Shimizu, R. (1978) Solution to a functional equation and its application to some characterization problems. Sankhya A40, 319–332.Google Scholar
Shimizu, R. (1979) On a lack of memory property of the exponential distribution. Ann. Inst. Statist. Math. 31, 309–313.Google Scholar