Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Geluk, J. L.
and
Pakes, A. G.
1991.
Second order subexponential distributions.
Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics,
Vol. 51,
Issue. 1,
p.
73.
Willekens, E.
and
Teugels, J. L.
1992.
Asymptotic expansions for waiting time probabilities in an M/G/1 queue with long-tailed service time.
Queueing Systems,
Vol. 10,
Issue. 4,
p.
295.
Kalashnikov, Vladimir
1997.
Geometric Sums: Bounds for Rare Events with Applications.
p.
30.
Kalashnikov, V.
and
Tsitsiashvili, G.
2001.
Asymptotically Correct Bounds of Geometric Convolutions with Subexponential Components.
Journal of Mathematical Sciences,
Vol. 106,
Issue. 2,
p.
2806.
Lin, Jianxi
and
Wang, Yuebao
2012.
New examples of heavy-tailed O-subexponential distributions and related closure properties.
Statistics & Probability Letters,
Vol. 82,
Issue. 3,
p.
427.
Gao, Qingwu
Liu, Yu
Psarrakos, Georgios
and
Wang, Yuebao
2013.
On asymptotic equivalence among the solutions of some defective renewal equations.
Lithuanian Mathematical Journal,
Vol. 53,
Issue. 4,
p.
391.
Chen, Wei
Yu, Changjun
and
Wang, Yuebao
2013.
Some discussions on the local distribution classes.
Statistics & Probability Letters,
Vol. 83,
Issue. 7,
p.
1654.
Xu, Hui
Foss, Sergey
and
Wang, Yuebao
2015.
Convolution and convolution-root properties of long-tailed distributions.
Extremes,
Vol. 18,
Issue. 4,
p.
605.
Cui, Zhaolei
Omey, Edward
Wang, Wenyuan
and
Wang, Yuebao
2018.
Asymptotics of convolution with the semi-regular-variation tail and its application to risk.
Extremes,
Vol. 21,
Issue. 4,
p.
509.
Wang, Yuebao
Xu, Hui
Cheng, Dongya
and
Yu, Changjun
2018.
The local asymptotic estimation for the supremum of a random walk with generalized strong subexponential summands.
Statistical Papers,
Vol. 59,
Issue. 1,
p.
99.
Xu, Hui
Cheng, Fengyang
Wang, Yuebao
and
Cheng, Dongya
2018.
A necessary and sufficient condition for the subexponentiality of the product convolution.
Advances in Applied Probability,
Vol. 50,
Issue. 01,
p.
57.
Leipus, Remigijus
Šiaulys, Jonas
and
Konstantinides, Dimitrios
2023.
Closure Properties for Heavy-Tailed and Related Distributions.
p.
7.

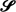 if the ratio of 1 –
if the ratio of 1 – 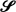 is used to prove that a certain class of functions previously thought to be contained in
is used to prove that a certain class of functions previously thought to be contained in 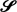 has members outside of
has members outside of 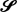 . Sufficient conditions on the tail of
. Sufficient conditions on the tail of  ; these conditions generalize previously published conditions.
; these conditions generalize previously published conditions.