Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Stoyanov, Jordan
and
Tolmatz, Leonid
2004.
New Stieltjes classes involving generalized gamma distributions.
Statistics & Probability Letters,
Vol. 69,
Issue. 2,
p.
213.
Mnatsakanov, Robert
and
Ruymgaart, Frits H.
2005.
Some results for moment-empirical cumulative distribution functions.
Journal of Nonparametric Statistics,
Vol. 17,
Issue. 6,
p.
733.
Ostrovska, Sofiya
and
Stoyanov, Jordan
2005.
Stieltjes classes for M-indeterminate powers of inverse Gaussian distributions.
Statistics & Probability Letters,
Vol. 71,
Issue. 2,
p.
165.
Stoyanov, Jordan
and
Tolmatz, Leonid
2005.
Method for constructing Stieltjes classes for M-indeterminate probability distributions.
Applied Mathematics and Computation,
Vol. 165,
Issue. 3,
p.
669.
Bisgaard, Torben Maack
and
Sasvári, Zoltán
2006.
When does imply independence?.
Statistics & Probability Letters,
Vol. 76,
Issue. 11,
p.
1111.
Lasserre, J. B.
Prieto‐Rumeau, T.
and
Zervos, M.
2006.
PRICING A CLASS OF EXOTIC OPTIONS VIA MOMENTS AND SDP RELAXATIONS.
Mathematical Finance,
Vol. 16,
Issue. 3,
p.
469.
Pakes, Anthony G.
2007.
Structure of Stieltjes classes of moment-equivalent probability laws.
Journal of Mathematical Analysis and Applications,
Vol. 326,
Issue. 2,
p.
1268.
Casas, Isabel
and
Gao, Jiti
2008.
Econometric estimation in long-range dependent volatility models: Theory and practice.
Journal of Econometrics,
Vol. 147,
Issue. 1,
p.
72.
Jones, M.C.
and
Arnold, Barry C.
2008.
Distributions that are both log-symmetric and R-symmetric.
Electronic Journal of Statistics,
Vol. 2,
Issue. none,
López-García, Marcos
2009.
Characterization of solutions to the Stieltjes–Wigert moment problem.
Statistics & Probability Letters,
Vol. 79,
Issue. 10,
p.
1337.
Ostrovska, Sofiya
and
Stoyanov, Jordan
2010.
A new proof that the product of three or more exponential random variables is moment-indeterminate.
Statistics & Probability Letters,
Vol. 80,
Issue. 9-10,
p.
792.
Stoyanov, Jordan
and
Lin, Gwo Dong
2011.
Mixtures of power series distributions: identifiability via uniqueness in problems of moments.
Annals of the Institute of Statistical Mathematics,
Vol. 63,
Issue. 2,
p.
291.
Stoyanov, Jordan
2012.
Inference Problems Involving Moment Determinacy of Distributions.
Communications in Statistics - Theory and Methods,
Vol. 41,
Issue. 16-17,
p.
2864.
Headrick, Todd C.
and
Pant, Mohan D.
2012.
On the Order Statistics of Standard Normal-Based Power Method Distributions.
ISRN Applied Mathematics,
Vol. 2012,
Issue. ,
p.
1.
Stoyanov, J
Stoyanov, J
Lin, G D
and
Lin, G D
2012.
Hardy's condition in the moment problem for probability distributions.
Теория вероятностей и ее применения,
Vol. 57,
Issue. 4,
p.
811.
Kleiber, Christian
and
Stoyanov, Jordan
2013.
Multivariate distributions and the moment problem.
Journal of Multivariate Analysis,
Vol. 113,
Issue. ,
p.
7.
Kleiber, Christian
2013.
On moment indeterminacy of the Benini income distribution.
Statistical Papers,
Vol. 54,
Issue. 4,
p.
1121.
Olteanu, Octav
2013.
New Results on Markov Moment Problem.
International Journal of Analysis,
Vol. 2013,
Issue. ,
p.
1.
Olteanu, Octav
2013.
Moment Problems on Bounded and Unbounded Domains.
International Journal of Analysis,
Vol. 2013,
Issue. ,
p.
1.
Stoyanov, J.
and
Lin, G. D.
2013.
Hardy's Condition in the Moment Problem for Probability Distributions.
Theory of Probability & Its Applications,
Vol. 57,
Issue. 4,
p.
699.
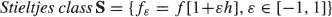 , where h is a ‘small' perturbation function. Such a class S consists of different distributions Fε (fε is the density of Fε ) all sharing the same moments as those of F, thus illustrating the nonuniqueness of F, and of any Fε, in terms of the moments. Power transformations of distributions such as the normal, log-normal and exponential are considered and for them Stieltjes classes written explicitly. We define a characteristic of S called an index of dissimilarity and calculate its value in some cases. A new Stieltjes class involving a power of the normal distribution is presented. An open question about the inverse Gaussian distribution is formulated. Related topics are briefly discussed.
, where h is a ‘small' perturbation function. Such a class S consists of different distributions Fε (fε is the density of Fε ) all sharing the same moments as those of F, thus illustrating the nonuniqueness of F, and of any Fε, in terms of the moments. Power transformations of distributions such as the normal, log-normal and exponential are considered and for them Stieltjes classes written explicitly. We define a characteristic of S called an index of dissimilarity and calculate its value in some cases. A new Stieltjes class involving a power of the normal distribution is presented. An open question about the inverse Gaussian distribution is formulated. Related topics are briefly discussed.
