Hostname: page-component-cd9895bd7-7cvxr Total loading time: 0 Render date: 2024-12-27T11:06:04.798Z Has data issue: false hasContentIssue false
  • English
  • Français

Almost sure convergence in Markov branching processes with infinite mean

Published online by Cambridge University Press:  14 July 2016

D. R. Grey
D. R. Grey*
Affiliation:
University of Sheffield
Get access Rights & Permissions [Opens in a new window]

Abstract

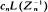If {Zn} is a Galton–Watson branching process with infinite mean, it is shown that under certain conditions there exist constants {cn} and a function L, slowly varying at 0, such that converges almost surely to a non-degenerate random variable, whose distribution function satisfies a certain functional equation. The method is then extended to a continuous-time Markov branching process {Zt} with infinite mean, where it is shown that there is always a function φ, slowly varying at 0, such that 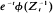converges almost surely to a non-degenerate random variable, and a necessary and sufficient condition is given for this convergence to be equivalent to convergence of 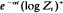for some constant α > 0.

Keywords

GALTON-WATSON PROCESSMARKOV BRANCHING PROCESSINFINITE MEANALMOST SURE CONVERGENCEMARTINGALESCONTINUOUS-TIME MARTINGALESSLOWLY VARYING FUNCTIONSFUNCTIONAL EQUATIONS
Type
Research Papers
Information
Journal of Applied Probability , Volume 14 , Issue 4 , December 1977 , pp. 702 - 716
Copyright
Copyright © Applied Probability Trust 1977 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1] Athreya, K. B. and Ney, P. E. (1972) Branching Processes. Springer-Verlag, Berlin.Google Scholar
[2] Bojanic, R. and Seneta, E. (1971) Slowly varying functions and asymptotic relations. J. Math. Anal. Appl. 34, 302–315.Google Scholar
[3] Cohn, H. (1977) Almost sure convergence of branching processes. Z. Wahrscheinlichkeitsth. 38, 73–81Google Scholar
[4] Darling, D. A. (1970) The Galton-Watson process with infinite mean. J. Appl. Prob. 7, 455–456.Google Scholar
[5] Doob, J. L. (1953) Stochastic Processes. Wiley, New York.Google Scholar
[6] Grey, D. R. (1974) Some Aspects of the Theory of Branching Processes. , University of Oxford.Google Scholar
[7] Grey, D. R. (1974) Asymptotic behaviour of continuous time, continuous state-space branching processes. J. Appl. Prob. 11, 669–677.Google Scholar
[8] Heyde, C. C. (1970) Extension of a result of Seneta for the supercritical Galton-Watson process. Ann. Math. Statist. 41, 739–742.Google Scholar
[9] Kesten, H. and Stigum, B. P. (1966) A limit theorem for multidimensional Galton-Watson processes. Ann. Math. Statist. 37, 1211–1223.Google Scholar
[10] Kuczma, M. (1964) Note on Schroder's functional equation. J. Austral. Math. Soc. 4, 149–151.Google Scholar
[11] Schuh, H.-J. and Barbour, A. D. (1977) On the asymptotic behaviour of branching processes with infinite mean. Adv. Appl. Prob. 9 (4) 681–723.Google Scholar
[12] Seneta, E. (1969) Functional equations and the Galton-Watson process. Adv. Appl. Prob. 1, 1–42.Google Scholar
[13] Seneta, E. (1973) The simple branching process with infinite mean I. J. Appl. Prob. 10, 206–212.Google Scholar
[14] Seneta, E. (1974) Regularly varying functions in the theory of simple branching processes. Adv. Appl. Prob. 6, 408–420.Google Scholar
[15] Szekeres, G. (1958) Regular iteration of real and complex functions. Acta Math. 100, 203–258.Google Scholar