Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
1979.
Discussion of the Paper by Professors Barndorff-Nielsen and Cox.
Journal of the Royal Statistical Society Series B: Statistical Methodology,
Vol. 41,
Issue. 3,
p.
299.
Hershey, John E.
and
Rao Yarlagadda, R. K.
1986.
Data Transportation and Protection.
p.
23.
Laendner, Stefan
Hehn, Thorsten
Milenkovic, Olgica
and
Huber, Johannes B.
2009.
The Trapping Redundancy of Linear Block Codes.
IEEE Transactions on Information Theory,
Vol. 55,
Issue. 1,
p.
53.

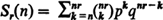 and
and 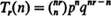 . Bounds for the remainder after
. Bounds for the remainder after 