An Extension of the Hájek-Rényi inequality for the case without moment conditions

Extract

In the paper [1], Hájek and Rényi established an inequality which they formulated in the following way: X₁,X₂,··· are independent random variables and 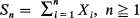. For each k, EX_k = 0 and 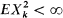, while 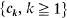is a non-increasing sequence of positive numbers. Then, for any ε > 0 and any positive integers n and m (n < m), 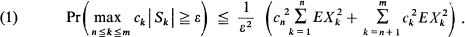The well-known Kolmogorov inequality is the particular case c_k = 1, all k, and n = 1 of (1). It is the object of the present note to produce an extended version of (1) where no moment conditions need be satisfied. This provides a useful general bound and illuminates the role of certain standard techniques in the study of the almost sure behaviour of sums of independent random variables.