Hostname: page-component-cd9895bd7-gxg78 Total loading time: 0 Render date: 2024-12-27T09:55:39.647Z Has data issue: false hasContentIssue false
  • English
  • Français

An optimal sequential policy for controlling a Markov renewal process

Published online by Cambridge University Press:  14 July 2016

J. M. McNamara
J. M. McNamara*
Affiliation:
University of Bristol
*
∗Postal address: School of Mathematics, University of Bristol, University Walk, Bristol BS8 1TW, UK.
Get access Rights & Permissions [Opens in a new window]

Abstract

This paper discusses a renewal process whose time development between renewals is described by a Markov process. The process may be controlled by choosing the times at which renewal occurs, the objective of the control being to maximise the long-term average rate of reward. Let γ ∗ denote the maximum achievable rate. We consider a specific policy in which a sequence of estimates 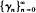of γ ∗ is made. This sequence is defined inductively as follows. Initially an (a priori)estimate γo is chosen. On making the nth renewal one estimates γ ∗ in terms of γo, the total rewards obtained in the first n renewal cycles and the total length of these cycles. γ n then determines the length of the (n + 1)th cycle. It is shown that γ n tends to γ ∗ as n tends to∞, and that this policy is optimal.

The time at which the (n + 1)th renewal is made is determined by solving a stopping problem for the Markov process with continuation cost γ n per unit time and stopping reward equal to the renewal reward. Thus, in general, implementation of this policy requires a knowledge of the transition probabilities of the Markov process. An example is presented in which one needs to know essentially nothing about the details of this process or the fine details of the reward structure in order to implement the policy. The example is based on a problem in biology.

Keywords

AVERAGE-COST OPTIMALITYRENEWAL REWARD PROCESSES
Type
Research Papers
Information
Journal of Applied Probability , Volume 22 , Issue 2 , June 1985 , pp. 324 - 335
Copyright
Copyright © Applied Probability Trust 1985 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bather, J. A. (1971) Free boundary problems in the design of control charts. Trans 6th Prague Conf. Information Theory, Statistical Decision Functions, Random Processes, Riedel, Dordrecht, 89–106.Google Scholar
Bather, J. A. (1977) On the sequential construction of an optimal age replacement policy. Bull. Internat. Statist. Inst. XLVII(2), 253–266.Google Scholar
Charnov, E. L. Optimal foraging: the marginal value theorem. Theoret. Popn Biol. 9, 129–136.CrossRefGoogle Scholar
Cowie, R. J. (1977) Optimal foraging in great tits (Parus major) . Nature 268, 137–139.CrossRefGoogle Scholar
Feller, W. (1971) An Introduction to Probability Theory and its Applications. Vol. 2, 2nd edn. Wiley, New York.Google Scholar
Gibb, J. A. (1960) Populations of tits and goldcrests and their food supply in pine plantations. Ibis 102, 163–208.CrossRefGoogle Scholar
Green, R. F. (1980) Bayesian birds: a simple example of Oaten's stochastic model of optimal foraging. Theoret. Popn Biol. 18, 244–256.CrossRefGoogle Scholar
Howard, R. A. (1960) Dynamic Programming and Markov Processes. MIT Press, Cambridge, MA.Google Scholar
Iwasa, Y., Higashi, M. and Yamamura, N. (1981) Prey distribution as a factor determining the choice of optimal foraging strategy. Amer. Nat. 117, 710–723.CrossRefGoogle Scholar
Johns, M. and Miller, R. G. (1963) Average renewal loss rate. Ann. Math. Statist. 34, 396–401.CrossRefGoogle Scholar
Krebs, J. R., Ryan, J. and Charnov, E. L. (1974) Hunting by expectation or optimal foraging? A study of patch use by chickadees. Anim. Behav. 22, 953–964.CrossRefGoogle Scholar
Lima, S. L. (1984) Downy woodpecker foraging behaviour: efficient sampling in simple stochastic environments. Ecology 65, 166–174.CrossRefGoogle Scholar
McNamara, J. M. (1982) Optimal patch use in a stochastic environment. Theoret. Popn Biol. 21, 269–288.CrossRefGoogle Scholar
Oaten, A. (1977) Optimal foraging in patches: a case for stochasticity. Theoret. Popn Biol. 12, 263–285.CrossRefGoogle ScholarPubMed
Whitham, T. G. (1977) Coevolution of foraging in Bombus — nectar dispensing Chilopsis: a last dreg theory. Science 197, 593–596.CrossRefGoogle ScholarPubMed