Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Sarkar, S.
Ma, W. T.
and
Sandri, G. v. H.
1992.
On fluctuation analysis: a new, simple and efficient method for computing the expected number of mutants.
Genetica,
Vol. 85,
Issue. 2,
p.
173.
Pakes, Anthony G.
1993.
Remarks on the Luria–Delbrück distribution.
Journal of Applied Probability,
Vol. 30,
Issue. 4,
p.
991.
Pakes, Anthony G.
1993.
Remarks on the Luria–Delbrück distribution.
Journal of Applied Probability,
Vol. 30,
Issue. 04,
p.
991.
Jones, M.E.
Wheldrake, J.
and
Rogers, A.
1993.
Luria-Delbrück fluctuation analysis: Estimating the Poisson parameter in a compound Poisson distribution.
Computers in Biology and Medicine,
Vol. 23,
Issue. 6,
p.
525.
Kemp, Adrienne W.
1994.
Comments on the Luria–Delbrück distribution.
Journal of Applied Probability,
Vol. 31,
Issue. 03,
p.
822.
Kemp, Adrienne W.
1994.
Comments on the Luria–Delbrück distribution.
Journal of Applied Probability,
Vol. 31,
Issue. 3,
p.
822.
Boe, L
Tolker-Nielsen, T
Eegholm, K M
Spliid, H
and
Vrang, A
1994.
Fluctuation analysis of mutations to nalidixic acid resistance in Escherichia coli.
Journal of Bacteriology,
Vol. 176,
Issue. 10,
p.
2781.
Kimmel, Marek
and
Axelrod, David E.
1994.
Fluctuation test for two-stage mutations: application to gene amplification.
Mutation Research/Fundamental and Molecular Mechanisms of Mutagenesis,
Vol. 306,
Issue. 1,
p.
45.
Jaeger, Gregg
and
Sarkar, Sahotra
1995.
On the distribution of bacterial mutants: The effects of differential fitness of mutants and non-mutants.
Genetica,
Vol. 96,
Issue. 3,
p.
217.
Rossman, Toby G.
Goncharova, Ekaterina I.
and
Nádas, Arthur
1995.
Modeling and measurement of the spontaneous mutation rate in mammalian cells.
Mutation Research/Fundamental and Molecular Mechanisms of Mutagenesis,
Vol. 328,
Issue. 1,
p.
21.
Nádas, Arthur
Goncharova, Ekaterina I.
and
Rossman, Toby G.
1996.
Mutations and infinity: Improved statistical methods for estimating spontaneous rates.
Environmental and Molecular Mutagenesis,
Vol. 28,
Issue. 2,
p.
90.
Sniegowski, Paul D.
Gerrish, Philip J.
and
Lenski, Richard E.
1997.
Evolution of high mutation rates in experimental populations of E. coli.
Nature,
Vol. 387,
Issue. 6634,
p.
703.
Elena, Santiago F.
and
Lenski, Richard E.
1997.
LONG‐TERM EXPERIMENTAL EVOLUTION IN
ESCHERICHIA COLI.
VII. MECHANISMS MAINTAINING GENETIC VARIABILITY WITHIN POPULATIONS
.
Evolution,
Vol. 51,
Issue. 4,
p.
1058.
Zheng, Qi
1999.
Progress of a half century in the study of the Luria–Delbrück distribution.
Mathematical Biosciences,
Vol. 162,
Issue. 1-2,
p.
1.
Rosche, William A.
and
Foster, Patricia L.
2000.
Determining Mutation Rates in Bacterial Populations.
Methods,
Vol. 20,
Issue. 1,
p.
4.
Angerer, Wolfgang P.
2001.
A note on the evaluation of fluctuation experiments.
Mutation Research/Fundamental and Molecular Mechanisms of Mutagenesis,
Vol. 479,
Issue. 1-2,
p.
207.
Kimmel, Marek
and
Axelrod, David E.
2002.
Branching Processes in Biology.
Vol. 19,
Issue. ,
p.
179.
Shaver, Aaron C
Dombrowski, Peter G
Sweeney, Joseph Y
Treis, Tania
Zappala, Renata M
and
Sniegowski, Paul D
2002.
Fitness Evolution and the Rise of Mutator Alleles in Experimental Escherichia coli Populations.
Genetics,
Vol. 162,
Issue. 2,
p.
557.
Zheng, Qi
2002.
Statistical and algorithmic methods for fluctuation analysis with SALVADOR as an implementation.
Mathematical Biosciences,
Vol. 176,
Issue. 2,
p.
237.
Shaver, Aaron C.
and
Sniegowski, Paul D.
2003.
Spontaneously Arising
mutL
Mutators in Evolving
Escherichia coli
Populations Are the Result of Changes in Repeat Length
.
Journal of Bacteriology,
Vol. 185,
Issue. 20,
p.
6076.

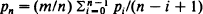 where
where 