Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Wang, Dingcheng
and
Tang, Qihe
2004.
Maxima of sums and random sums for negatively associated random variables with heavy tails.
Statistics & Probability Letters,
Vol. 68,
Issue. 3,
p.
287.
Geluk, Jaap
and
Ng, Kai W.
2006.
Tail behavior of negatively associated heavy-tailed sums.
Journal of Applied Probability,
Vol. 43,
Issue. 02,
p.
587.
Wang, Yuebao
Yang, Yang
Wang, Kaiyong
and
Cheng, Dongya
2007.
Some new equivalent conditions on asymptotics and local asymptotics for random sums and their applications.
Insurance: Mathematics and Economics,
Vol. 40,
Issue. 2,
p.
256.
Kong, Fanchao
and
Zong, Gaofeng
2008.
The finite-time ruin probability for ND claims with constant interest force.
Statistics & Probability Letters,
Vol. 78,
Issue. 17,
p.
3103.
Chen, Guochun
Wang, Yuebao
and
Cheng, Fengyang
2009.
The Uniform Local Asymptotics of the Overshoot of a Random Walk with Heavy-Tailed Increments.
Stochastic Models,
Vol. 25,
Issue. 3,
p.
508.
Wang, Yuebao
and
Wang, Kaiyong
2011.
Random walks with non-convolution equivalent increments and their applications.
Journal of Mathematical Analysis and Applications,
Vol. 374,
Issue. 1,
p.
88.
Liu, Yan
and
Tang, QiHe
2011.
Heavy tails of a Lévy process and its maximum over a random time interval.
Science China Mathematics,
Vol. 54,
Issue. 9,
p.
1875.
Yuen, Kam Chuen
and
Yin, Chuancun
2012.
Asymptotic results for tail probabilities of sums of dependent and heavy-tailed random variables.
Chinese Annals of Mathematics, Series B,
Vol. 33,
Issue. 4,
p.
557.
Lin, Zhengyan
and
Shen, Xinmei
2013.
Approximation of the Tail Probability of Dependent Random Sums Under Consistent Variation and Applications.
Methodology and Computing in Applied Probability,
Vol. 15,
Issue. 1,
p.
165.
Chen, Wei
Yu, Changjun
and
Wang, Yuebao
2013.
Some discussions on the local distribution classes.
Statistics & Probability Letters,
Vol. 83,
Issue. 7,
p.
1654.
Cui, Zhaolei
Wang, Yuebao
and
Wang, Kaiyong
2016.
The uniform local asymptotics for a Lévy process and its overshoot and undershoot.
Communications in Statistics - Theory and Methods,
Vol. 45,
Issue. 4,
p.
1156.
Bloznelis, Mindaugas
2019.
Local probabilities of randomly stopped sums of power-law lattice random variables.
Lithuanian Mathematical Journal,
Vol. 59,
Issue. 4,
p.
437.
Jiang, Tao
Wang, Yuebao
Cui, Zhaolei
and
Chen, Yuxin
2019.
On the almost decrease of a subexponential density.
Statistics & Probability Letters,
Vol. 153,
Issue. ,
p.
71.

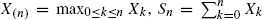 and
and 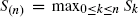 for
for 