Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
El-Shehawy, Ahmed
1992.
On absorption probabilities for a random walk between two different barriers.
Annales de la Faculté des sciences de Toulouse : Mathématiques,
Vol. 1,
Issue. 1,
p.
95.
Stadje, Wolfgang
1992.
The expected value of the one-sided cusum stopping time.
Advances in Applied Probability,
Vol. 24,
Issue. 4,
p.
1008.
Khan, Rasul A.
1995.
Detecting changes in probabilities of a multi—component process.
Sequential Analysis,
Vol. 14,
Issue. 4,
p.
375.
Bulinskaya, Ekaterina V.
1996.
Operations Research Proceedings 1995.
Vol. 1995,
Issue. ,
p.
451.
Bulinskaya, E.V
1996.
Stability problems in inventory theory.
International Journal of Production Economics,
Vol. 45,
Issue. 1-3,
p.
353.
Bulinskaya, E. V.
1998.
System stability and optimal control.
Journal of Mathematical Sciences,
Vol. 92,
Issue. 3,
p.
3857.
Lotov, V. I.
1999.
On hitting the high level by a random walk with delay at the origin.
Siberian Mathematical Journal,
Vol. 40,
Issue. 6,
p.
1079.
Stadje, W.
2002.
The Embedded Random Walk in the Stationary M/M/1 Queue.
Methodology And Computing In Applied Probability,
Vol. 4,
Issue. 2,
p.
143.
Stadje, Wolfgang
2002.
FIRST-PASSAGE TIMES FOR SOME LINDLEY PROCESSES IN CONTINUOUS TIME.
Sequential Analysis,
Vol. 21,
Issue. 1-2,
p.
87.

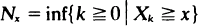 . These stopping times are used in Page's (1954) one-sided cusum procedures and are also important in queueing theory. Various asymptotic properties of
. These stopping times are used in Page's (1954) one-sided cusum procedures and are also important in queueing theory. Various asymptotic properties of 