Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Matsui, Muneya
2014.
Prediction in a non-homogeneous Poisson cluster model.
Insurance: Mathematics and Economics,
Vol. 55,
Issue. ,
p.
10.
Matsui, Muneya
2015.
Prediction in a Poisson cluster model with multiple cluster processes.
Scandinavian Actuarial Journal,
Vol. 2015,
Issue. 1,
p.
1.
Matsui, Muneya
and
Rolski, Tomasz
2016.
Prediction in a mixed Poisson cluster model.
Stochastic Models,
Vol. 32,
Issue. 3,
p.
460.
Matsui, Muneya
2017.
Prediction of Components in Random Sums.
Methodology and Computing in Applied Probability,
Vol. 19,
Issue. 2,
p.
573.

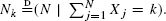 In particular, we want to know the asymptotic behavior of the conditional mean E
In particular, we want to know the asymptotic behavior of the conditional mean E