Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-27T06:05:43.506Z Has data issue: false hasContentIssue false
  • English
  • Français

A Central Limit Theorem for Contractive Stochastic Dynamical Systems

Part of: Markov processes Limit theorems

Published online by Cambridge University Press:  14 July 2016

Martin Benda
Martin Benda*
Affiliation:
Universität München
*
∗Postal address: Mathematisches Institut, Universität München, Theresienstrasse 39, D-80333, München, Germany
Get access Rights & Permissions [Opens in a new window]

Abstract

If (Fn)n∈ℕ is a sequence of independent and identically distributed random mappings from a second countable locally compact state space 𝕏 to 𝕏 which itself is independent of the 𝕏-valued initial variable X0, the discrete-time stochastic process (Xn)n≥0, defined by the recursion equation Xn = Fn(Xn−1) for n∈ℕ, has the Markov property. Since 𝕏 is Polish in particular, a complete metric d exists. The random mappings (Fn)n∈ℕ are assumed to satisfy ℙ-a.s. 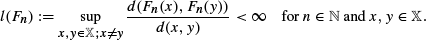Conditions on the distribution of l(Fn) are given for the existence of an invariant distribution of X0 making the process (Xn)n≥0 stationary and ergodic. Our main result corrects a central limit theorem by Łoskot and Rudnicki (1995) and removes an error in its proof. Instead of trying to compare the sequence φ (Xn)n≥0 for some φ : 𝕏 → ℝ with a triangular scheme of independent random variables our proof is based on an approximation by a martingale difference scheme.

Keywords

Markov chaininvariant distributioncentral limit theoremiterated function system

MSC classification

Primary: 60J05: Discrete-time Markov processes on general state spaces
Secondary: 60F05: Central limit and other weak theorems
Type
Short Communications
Information
Journal of Applied Probability , Volume 35 , Issue 1 , March 1998 , pp. 200 - 205
Copyright
Copyright © Applied Probability Trust 1998 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Billingsley, P. (1961). The Lindeberg–Levy theorem for martingales. Proc. Amer. Math. Soc. 12, 788–792.Google Scholar
Elton, J. (1990). A multiplicative ergodic theorem for Lipschitz maps. Stoch. Proc. Appl. 34, 39–47.Google Scholar
Loskot, K., and Rudnicki, R. (1995). Limit theorems for stochastically perturbed systems. J. Appl. Prob. 32, 459–469.Google Scholar