Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Cacoullos, Theophilos
and
Papageorgiou, H.
1982.
Characterizing the negative binomial distribution.
Journal of Applied Probability,
Vol. 19,
Issue. 03,
p.
742.
Henery, Robert J.
1983.
Permutation probabilities for gamma random variables.
Journal of Applied Probability,
Vol. 20,
Issue. 04,
p.
822.
Zijlstra, Mynt
1983.
Characterizations of the geometric distribution by distributional properties.
Journal of Applied Probability,
Vol. 20,
Issue. 04,
p.
843.
Abdul-Razak, Rafid S
and
Patil, Ganapati P
1986.
Power series distributions and their conjgates in stochastic modeling and baysian inference.
Communications in Statistics - Theory and Methods,
Vol. 15,
Issue. 3,
p.
623.
Rego, Vernon
1988.
Some explicit formulas for mixed exponential service systems.
Computers & Operations Research,
Vol. 15,
Issue. 6,
p.
509.
Rego, Vernon
and
Szpankowski, Wojciech
1989.
The presence of exponentiality in entropy maximized M/GI/1 queues.
Computers & Operations Research,
Vol. 16,
Issue. 5,
p.
441.
Xekalaki, E.
and
Panaretos, J.
1989.
On the Association of the Pareto and the Yule Distribution.
Theory of Probability & Its Applications,
Vol. 33,
Issue. 1,
p.
191.
Sim, C. H.
and
Lee, P. A.
1989.
Simulation of negative binomial processes.
Journal of Statistical Computation and Simulation,
Vol. 34,
Issue. 1,
p.
29.
Panaretos, J.
1991.
On the duality of certain characterizations of the exponential and the geometric distributions.
p.
156.
Ong, S. H.
1995.
Characterization of the Negative Binomial and Gamma Distributions.
Biometrical Journal,
Vol. 37,
Issue. 2,
p.
251.
Gharib, M.
1995.
Two characterisations of a gamma mixture distribution.
Bulletin of the Australian Mathematical Society,
Vol. 52,
Issue. 3,
p.
353.
Gharib, M.
1996.
Characterizations of the exponential distribution via mixing distributions.
Microelectronics Reliability,
Vol. 36,
Issue. 3,
p.
293.
Wesołowski, Jacek
and
Ahsanullah, Mohammad
1998.
Distributional Properties of Exceedance Statistics.
Annals of the Institute of Statistical Mathematics,
Vol. 50,
Issue. 3,
p.
543.
AHN, SUNEUNG
and
KIM, WOOHYUN
2008.
SERVICE LEVEL ANALYSIS OF (S - 1, S) INVENTORY POLICY FOR NEGATIVE BINOMIAL DISTRIBUTED FAILURES.
Asia-Pacific Journal of Operational Research,
Vol. 25,
Issue. 06,
p.
827.
Vellaisamy, P.
and
Upadhye, N. S.
2009.
On the Sums of Compound Negative Binomial and Gamma Random Variables.
Journal of Applied Probability,
Vol. 46,
Issue. 01,
p.
272.
Vellaisamy, P.
and
Sreehari, M.
2010.
Some Intrinsic Properties of the Gamma Distribution.
JOURNAL OF THE JAPAN STATISTICAL SOCIETY,
Vol. 40,
Issue. 1,
p.
133.

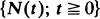 there exists a one-to-one relation between the distribution of the random variable
there exists a one-to-one relation between the distribution of the random variable 