Hostname: page-component-78c5997874-s2hrs Total loading time: 0 Render date: 2024-11-10T21:58:00.233Z Has data issue: false hasContentIssue false
  • English
  • Français

The closure of a local subexponential distribution class under convolution roots, with applications to the compound Poisson process

Part of: Distribution theory - Probability Limit theorems

Published online by Cambridge University Press:  14 July 2016

Yuebao Wang ,
Dongya Cheng  and
Kaiyong Wang
Yuebao Wang*
Affiliation:
Soochow University
Dongya Cheng*
Affiliation:
Soochow University
Kaiyong Wang*
Affiliation:
Soochow University
*
∗Postal address: Department of Mathematics, Soochow University, Suzhou, 215006, P. R. China.
∗Postal address: Department of Mathematics, Soochow University, Suzhou, 215006, P. R. China.
∗Postal address: Department of Mathematics, Soochow University, Suzhou, 215006, P. R. China.
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

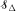Let denote the class of local subexponential distributions and 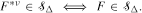F∗ν the ν-fold convolution of distribution F, where ν belongs to one of the following three cases: ν is a random variable taking only a finite number of values, in particular ν ≡ n for some n ≥ 2; ν is a Poisson random variable; or ν is a geometric random variable. Along the lines of Embrechts, Goldie, and Veraverbeke (1979), the following assertion is proved under certain conditions: This result is applied to the infinitely divisible laws and some new results are established. The results obtained extend the corresponding findings of Asmussen, Foss, and Korshunov (2003).

Keywords

Local subexponential distribution classconvolution rootcompound Poisson processinfinitely divisible law

MSC classification

Primary: 60E05: Distributions
Secondary: 60F99: None of the above, but in this section
Type
Research Papers
Information
Journal of Applied Probability , Volume 42 , Issue 4 , December 2005 , pp. 1194 - 1203
Copyright
© Applied Probability Trust 2005 

References

Asmussen, S., Foss, S. and Korshunov, D. (2003). Asymptotics for sums of random variables with local subexponential behavior. J. Theoret. Prob. 16, 489–518.Google Scholar
Embrechts, P. and Goldie, C. M. (1982). On convolution tails. Stoch. Process. Appl. 13, 263–270.Google Scholar
Embrechts, P., Goldie, C. M. and Veraverbeke, N. (1979). Subexponentiality and infinite divisibility. Z. Wahrscheinlichkeitsth. 49, 335–347.Google Scholar
Feller, W. (1971). An Introduction to Probability Theory and Its Applications, Vol. 2, 2nd edn. John Wiley, New York.Google Scholar