Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Bosch, K.
and
Jensen, U.
1983.
Instandhaltungsmodelle — Eine Übersicht.
Operations-Research-Spektrum,
Vol. 5,
Issue. 3,
p.
129.
Griffith, William S.
2004.
Encyclopedia of Statistical Sciences.
Griffith, William S.
2005.
Encyclopedia of Statistical Sciences.
Griffith, William S.
2014.
Wiley StatsRef: Statistics Reference Online.
Griffith, William S.
2015.
Wiley StatsRef: Statistics Reference Online.
p.
1.
Zhao, Xian
Guo, Xiaoxin
and
Wang, Xiaoyue
2018.
Reliability and maintenance policies for a two-stage shock model with self-healing mechanism.
Reliability Engineering & System Safety,
Vol. 172,
Issue. ,
p.
185.

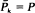 [the device survives
[the device survives 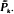 . A counterexample to the IFR preservation theorem is given in which
. A counterexample to the IFR preservation theorem is given in which 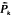 is strictly IFR while the failure rate is initially decreasing and then increasing.
is strictly IFR while the failure rate is initially decreasing and then increasing.