Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2024-12-28T03:37:11.567Z Has data issue: false hasContentIssue false
  • English
  • Français

A clustering law for some discrete order statistics

Part of: Nonparametric inference

Published online by Cambridge University Press:  14 July 2016

Sunder Sethuraman
Sunder Sethuraman*
Affiliation:
Iowa State University
*
∗ Postal address: 400 Carver Hall, Department of Mathematics, Iowa State University, Ames, IA 50011, USA. Email address: sethuram@iastate.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

Let X1, X2, …, Xn be a sequence of independent, identically distributed positive integer random variables with distribution function F. Anderson (1970) proved a variant of the law of large numbers by showing that the sample maximum moves asymptotically on two values if and only if F satisfies a ‘clustering’ condition, 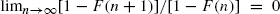In this article, we generalize Anderson's result and show that it is robust by proving that, for any r ≥ 0, the sample maximum and other extremes asymptotically cluster on r + 2 values if and only if 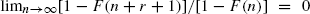Together with previous work which considered other asymptotic properties of these sample extremes, a more detailed asymptotic clustering structure for discrete order statistics is presented.

Keywords

Order statisticslaw of large numbersextremesasymptoticsclustering

MSC classification

Primary: 62G32: Statistics of extreme values; tail inference
Type
Research Papers
Information
Journal of Applied Probability , Volume 40 , Issue 1 , March 2003 , pp. 226 - 241
Copyright
Copyright © Applied Probability Trust 2003 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

Research supported in part by NSF grant DMS-00711504.

References

Anderson, C. W. (1970). Extreme value theory for a class of discrete distributions with applications. J. Appl. Prob. 7, 99–113.CrossRefGoogle Scholar
Athreya, J. S., and Sethuraman, S. (2001). On the asymptotics of discrete order statistics. Statist. Prob. Lett. 54, 243–249.Google Scholar
Baryshnikov, Y., Eisenberg, B., and Stengle, G. (1995). A necessary and sufficient condition for the existence of the limiting probability of a tie for first place. Statist. Prob. Lett. 23, 203–209.Google Scholar
Galambos, J. (1987). The Asymptotic Theory of Extreme Order Statistics. Krieger, Melbourne, FL.Google Scholar
Gnedenko, B. V. (1943). Sur la distribution limite du terme maximum d'une série aléatoire. Ann. Math. 44, 423–453.Google Scholar