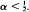Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Winter, B.B.
1981.
Fourier series methods in nonparametric estimation.
Series Statistics,
Vol. 12,
Issue. 3,
p.
339.
Cheng, K. F.
1982.
Contributions to nonparametric generalized failure rate function estimation.
Metrika,
Vol. 29,
Issue. 1,
p.
215.
Falk, M.
1983.
Relative efficiency and deficiency of kernel type estimators of smooth distribution functions.
Statistica Neerlandica,
Vol. 37,
Issue. 2,
p.
73.
1983.
Nonparametric Functional Estimation.
p.
483.
Singh, R.S.
Gasser, T.
and
Prasad, B.
1983.
Nonparametric estimates of distribution functions.
Communications in Statistics - Theory and Methods,
Vol. 12,
Issue. 18,
p.
2095.
Nixdorf, R.
1985.
CENTRAL LIMIT THEORMS IN C[0,1] FOR A CLASS OF ESTIMATORS OF A DISTRIBUTION FUNCTION.
Statistica Neerlandica,
Vol. 39,
Issue. 3,
p.
251.
Peter D., Hill
1985.
Kernel estimation of a distribution function.
Communications in Statistics - Theory and Methods,
Vol. 14,
Issue. 3,
p.
605.
Puri, Madan L
and
Ralescu, Stefan S
1986.
Central limit theorem for perturbed empirical distribution functions evaluated at a random point.
Journal of Multivariate Analysis,
Vol. 19,
Issue. 2,
p.
273.
Boos, D. D.
1986.
Rates of convergence for the distance between distribution function estimators.
Metrika,
Vol. 33,
Issue. 1,
p.
197.
Gajek, Les⌈aw
1987.
On improving distribution function estimators which are not monotonic functions.
Statistics & Probability Letters,
Vol. 5,
Issue. 3,
p.
213.
Swanepoel, Jan W.H.
1988.
Mean intergrated squared error properties and optimal kernels when estimating a diatribution function.
Communications in Statistics - Theory and Methods,
Vol. 17,
Issue. 11,
p.
3785.
Lea, Cheun-Der
and
Puri, Madan L.
1988.
Asymptotic properties of perturbed empirical distribution functions evaluated at a random point.
Journal of Statistical Planning and Inference,
Vol. 19,
Issue. 2,
p.
201.
Yukich, J.E.
1989.
A note on limit theorems for perturbed empirical processes.
Stochastic Processes and their Applications,
Vol. 33,
Issue. 1,
p.
163.
Mack, Y.P.
and
Matloff, Norman S.
1990.
Estimating a mixing distribution in a multiple observation setting.
Statistics & Probability Letters,
Vol. 10,
Issue. 5,
p.
369.
Ghorai, J. K.
and
Susarla, V.
1990.
Kernel estimation of a smooth distribution function based on censored data.
Metrika,
Vol. 37,
Issue. 1,
p.
71.
Sarda, P.
1991.
Nonparametric Functional Estimation and Related Topics.
p.
261.
Gröwe, N.
and
Römisch, W.
1992.
Proceedings of the Sixth European Conference on Mathematics in Industry August 27–31, 1991 Limerick.
p.
169.
Ralescu, Stefan S.
1992.
Asymptotic deviations between perturbed empirical and quantile processes.
Journal of Statistical Planning and Inference,
Vol. 32,
Issue. 2,
p.
243.
Gröwe, Nicole
and
Römisch, Werner
1992.
Stochastic Optimization.
Vol. 379,
Issue. ,
p.
111.
Lall, Upmanu
Moon, Young‐il
and
Bosworth, Ken
1993.
Kernel flood frequency estimators: Bandwidth selection and kernel choice.
Water Resources Research,
Vol. 29,
Issue. 4,
p.
1003.
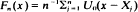 where Uo is the d.f. of the unit mass at zero. An admissible perturbation of the e.d.f., say
where Uo is the d.f. of the unit mass at zero. An admissible perturbation of the e.d.f., say 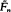 , is obtained if Uo is replaced by a d.f.
, is obtained if Uo is replaced by a d.f. 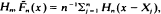 , where
, where 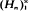 is a sequence of d.f.'s converging weakly to Uo. Such perturbed e.d.f.′s arise quite naturally as integrals of non-parametric density estimators, e.g. as
is a sequence of d.f.'s converging weakly to Uo. Such perturbed e.d.f.′s arise quite naturally as integrals of non-parametric density estimators, e.g. as 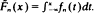 . It is shown that if F satisfies some smoothness conditions and the perturbation is not too drastic then
. It is shown that if F satisfies some smoothness conditions and the perturbation is not too drastic then 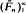 ‘has the Chung–Smirnov property'; i.e., with probability one,
‘has the Chung–Smirnov property'; i.e., with probability one, 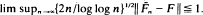 1. But if the perturbation is too vigorous then this property is lost: e.g., if F is the uniform distribution and Hn is the d.f. of the unit mass at n–α then the above lim sup is ≦ 1 or = ∞, depending on whether
1. But if the perturbation is too vigorous then this property is lost: e.g., if F is the uniform distribution and Hn is the d.f. of the unit mass at n–α then the above lim sup is ≦ 1 or = ∞, depending on whether 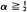 or
or