Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2024-12-27T21:10:21.915Z Has data issue: false hasContentIssue false
  • English
  • Français

Convergence to stationary state for a Markov move-to-front scheme

Part of: Markov processes Stochastic processes

Published online by Cambridge University Press:  14 July 2016

Eliane R. Rodrigues
Eliane R. Rodrigues*
Affiliation:
Universidade de Brasilia
*
∗Postal address: Universidade de Brasília, Departamento de Matemática, Campus Universitário, Asa Norte, 70.919–900, Brasilia DF, Brazil.
Get access Rights & Permissions [Opens in a new window]

Abstract

This work considers 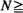items (e.g. books, files) arranged in an array (e.g. shelf, tape) with N positions and assumes that items are requested according to a Markov chain (possibly, of higher order). After use, the requested item is returned to the leftmost position of the array. Successive applications of the procedure above give rise to a Markov chain on permutations. For equally likely items, the number of requests that makes this Markov chain close to its stationary state is estimated. To achieve that, a coupling argument and the total variation distance are used. Finally, for non-equally likely items and so-called p-correlated requests, the coupling time is presented as a function of the coupling time when requests are independent.

Keywords

MARKOV AND HIGHER-ORDER MARKOV REQUESTSTIME TO STATIONARITYCOUPLINGTOTAL VARIATION DISTANCE

MSC classification

Primary: 60J20: Applications of Markov chains and discrete-time Markov processes on general state spaces (social mobility, learning theory, industrial processes, etc.)
Secondary: 60G10: Stationary processes
Type
Research Papers
Information
Journal of Applied Probability , Volume 32 , Issue 3 , September 1995 , pp. 768 - 776
Copyright
Copyright © Applied Probability Trust 1995 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

Most of this work was done while the author was doing her Ph.D. at Queen Mary and Westfield College, University of London, UK.

References

Aldous, D. (1989) Probability Approximations via the Poisson Clumping Heuristic. Applied Mathematical Sciences 77. Springer-Verlag, New York.Google Scholar
Aldous, D. and Diaconis, P. (1987) Strong stationary times and finite random walks. Adv. Appl. Math. 8, 69–97.Google Scholar
Baum, L. E. and Billingsley, P. (1965) Asymptotic distributions for the coupon-collector's problem. Ann. Math. Statist. 36, 1835–1839.Google Scholar
Diaconis, P. (1988) Group Representations in Probability and Statistics. Lecture Notes — Monograph Series Vol. 11. Institute of Mathematical Statistics.Google Scholar
Diaconis, P., Fill, J. A. and Pitman, J. (1992) Analysis of top to random shuffles. Combinatorics, Probability and Computing 1, 135–155.Google Scholar
Dobrow, R. P. (1994) The move-to-root self-organizing trees with Markov dependent requests. Preprint.Google Scholar
Dobrow, R. P. and Fill, J. A. (1994) The move-to-front rule for self-organizing lists with Markov dependent requests. Preprint.CrossRefGoogle Scholar
Doeblin, W. (1938) Exposé de la theorie des chaînes simples constantes de Markov à un nombre fini d'états. Rev. Math. de l'Union Interbalkanique 2, 77–105.Google Scholar
Feller, W. (1968) An Introduction to Probability Theory and its Applications, Vol. I, 3rd edn. Wiley, New York.Google Scholar
Fill, J. A. (1993) An exact formula for the move-to-front rule for self-organizing lists. Preprint.Google Scholar
Goldstein, D. (1979) Maximal coupling, Z. Wahrscheinlichkeitsth. 46, 193–204.Google Scholar
Griffeath, D. (1975) A maximal coupling for Markov chains. Z. Wahrscheinlichkeitsth. 31, 95–106.Google Scholar
Griffeath, D. (1978) Coupling methods for Markov processes. Studies in Probability and Ergodic Theory. Advances in Mathematics Supplementary Studies 2, 1–43.Google Scholar
Hendricks, W. J. (1972) The stationary distribution of an interesting Markov chain. J. Appl. Prob. 9, 231–233.Google Scholar
Lindvall, T. (1992) Lectures on the Coupling Method. Wiley, New York.Google Scholar
Rodrigues, E. R. (1993) A study of self-organising schemes and time to stationarity for some Markov processes. . Queen Mary and Westfield College, University of London.Google Scholar
Thorisson, H. (1986) On maximal and distributional coupling. Ann. Prob. 14, 873–876.CrossRefGoogle Scholar