Hostname: page-component-cd9895bd7-lnqnp Total loading time: 0 Render date: 2024-12-29T07:14:03.586Z Has data issue: false hasContentIssue false
  • English
  • Français

A coupling of finite particle systems

Part of: Special processes

Published online by Cambridge University Press:  14 July 2016

T. S. Mountford
T. S. Mountford*
Affiliation:
University of California, Los Angeles
*
∗ Postal address: Department of Mathematics, University of California, Los Angeles, CA 90024, USA.
Get access Rights & Permissions [Opens in a new window]

Abstract

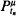We show that for a large class of one-dimensional interacting particle systems, with a finite initial configuration, any limit measure , for a sequence of times tending to infinity, must be invariant. This result is used to show that the one-dimensional biased annihilating branching process with parameter > 1/3 converges in distribution to the upper invariant measure provided its initial configuration is almost surely finite and non-null.

Keywords

CONTINUOUS-TIME MARKOV CHAININTERACTING PARTICLE SYSTEMINVARIANT MEASURE

MSC classification

Primary: 60K35: Interacting random processes; statistical mechanics type models; percolation theory
Type
Short Communications
Information
Journal of Applied Probability , Volume 30 , Issue 1 , March 1993 , pp. 258 - 262
Copyright
Copyright © Applied Probability Trust 1993 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

Research partially supported by NSF Grant DMS-9157461 and the Sloan Foundation.

References

Andjel, E., Bramson, M. and Liggett, M. (1988) Shocks in the asymmetric exclusion process. Prob. Theory Rel. Fields. 78, 231–247.Google Scholar
Durrett, R. (1990) Probability: Theory and Examples. Wadsworth, Pacific Grove, Ca.Google Scholar
Liggett, T. (1985) Interacting Particle Systems. Springer-Verlag, New York.Google Scholar
Neuhauser, C. and Sudbury, A. (1991) Biased annihilating branching processes. Adv. Appl. Prob. 25(1).Google Scholar
Sudbury, A. (1989) Geometric bounds for a particle moving under different random walk regimes. Preprint, Monash University.Google Scholar