Hostname: page-component-78c5997874-dh8gc Total loading time: 0 Render date: 2024-11-13T03:25:22.088Z Has data issue: false hasContentIssue false
  • English
  • Français

Exact simulation of generalised Vervaat perpetuities

Part of: Probabilistic methods, simulation and stochastic differential equations Special processes Stochastic processes

Published online by Cambridge University Press:  12 July 2019

Angelos Dassios ,
Yan Qu  and
Jia Wei Lim
Angelos Dassios*
Affiliation:
London School of Economics and Political Science
Yan Qu*
Affiliation:
London School of Economics and Political Science
Jia Wei Lim*
Affiliation:
University of Bristol
*
*Postal address: Department of Statistics, London School of Economics and Political Science, Houghton Street, London WC2A 2AE, UK.
*Postal address: Department of Statistics, London School of Economics and Political Science, Houghton Street, London WC2A 2AE, UK.
***Postal address: Department of Mathematics, University of Bristol, Senate House, Tyndall Avenue, Bristol BS8 1TH, UK.
Get access Rights & Permissions [Opens in a new window]

Abstract

We consider a generalised Vervaat perpetuity of the form X = Y1W1 +Y2W1W2 + · · ·, where 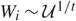$W_i \sim {\cal U}^{1/t}$ and (Yi)i≥0 is an independent and identically distributed sequence of random variables independent from (Wi)i≥0. Based on a distributional decomposition technique, we propose a novel method for exactly simulating the generalised Vervaat perpetuity. The general framework relies on the exact simulation of the truncated gamma process, which we develop using a marked renewal representation for its paths. Furthermore, a special case arises when Yi = 1, and X has the generalised Dickman distribution, for which we present an exact simulation algorithm using the marked renewal approach. In particular, this new algorithm is much faster than existing algorithms illustrated in Chi (2012), Cloud and Huber (2017), Devroye and Fawzi (2010), and Fill and Huber (2010), as well as being applicable to the general payments case. Examples and numerical analysis are provided to demonstrate the accuracy and effectiveness of our method.

Keywords

Vervaat perpetuityDickman distributiontruncated gamma processexact simulationmarked renewal process

MSC classification

Primary: 60G51: Processes with independent increments; L'evy processes
Secondary: 60K15: Markov renewal processes, semi-Markov processes 65C05: Monte Carlo methods
Type
Research Papers
Information
Journal of Applied Probability , Volume 56 , Issue 1 , March 2019 , pp. 57 - 75
Copyright
© Applied Probability Trust 2019 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Arratia, R. (1998). On the central role of scale invariant Poisson processes on (0, ∞). In Microsurveys in Discrete Probability, eds Aldous, D. and Propp, J., American Mathematical Society, pp. 21–41.CrossRefGoogle Scholar
Blanchet, J. H. and Sigman, K. (2011). On exact sampling of stochastic perpetuities. In Probability, Analysis and Number Theory (J. Appl. Prob. Spec. Vol. 48A), eds Goldie, C. M. and Mijatović, A., Applied Probability Trust, sheffield, pp. 165–182.Google Scholar
Chandrasekhar, S. and Münch, G. (1950). The theory of the fluctuations in brightness of the Milky Way, I and II. Astrophys. J. 112, 380–398.CrossRefGoogle Scholar
Chi, Z. (2012). On exact sampling of nonnegative infinitely divisible random variables. Anal. Appl. Prob. 44, 842–873.Google Scholar
Cloud, K. and Huber, M. (2017). Fast perfect simulation of Vervaat perpetuities. J. Complexity 42, 19–30.CrossRefGoogle Scholar
De Bruijn, N. (1951). The asymptotic behaviour of a function occurring in the theory of primes. J. Indian Math. Soc. 15, 20–32.Google Scholar
Devroye, L. (2001). Simulating perpetuities. Methodol. Comput. Appl. Probab. 3, 97–115.CrossRefGoogle Scholar
Devroye, L. and Fawzi, O. (2010). Simulating the Dickman distribution. Statist. Probab. Lett. 80, 242–247.CrossRefGoogle Scholar
Dickman, K. (1930). On the frequency of numbers containing prime factors of a certain relative magnitude. Arkiv for Matematik, Astronomi och Fysik 22, 1–14.Google Scholar
Embrechts, P. and Goldie, C. M. (1994). Perpetuities and random equations. In Asymptotic Statistics, eds Mandl, P. and Hušková, M., Springer, pp. 75–86.CrossRefGoogle Scholar
Embrechts, P., Klüppelberg, C. and Mikosch, T. (1996). Modelling Extremal Events. Springer.Google Scholar
Fill, J. and Huber, M. (2010). Perfect simulation of Vervaat perpetuities. Electron. J. Prob. 15, 96–109.10.1214/EJP.v15-734CrossRefGoogle Scholar
Goldie, C. M. and Grübel, R. (1996). Perpetuities with thin tails. Anal. Appl. Prob. 28, 463–480.Google Scholar
Grübel, R. and Rösler, U. (1996). Asymptotic distribution theory for Hoare’s selection algorithm. Anal. Appl. Prob. 28, 252–269.Google Scholar
Mahmoud, H.M., Modarres, R. and Smythe, R.T. (1995). Analysis of Quickselect: an algorithm for order statistics. RAIRO Theoret. Inform. Appl. 29, 255–276.CrossRefGoogle Scholar
Nyrhinen, H. (2001). Finite and infinite time ruin probabilities in a stochastic economics environment. Stoch. Proc. Appl. 92, 265–285.10.1016/S0304-4149(00)00083-1CrossRefGoogle Scholar
Takács, L. (1954). On secondary processes generated by a Poisson process and their applications in physics. Acta Math. Hungar. 5, 203–236.10.1007/BF02020410CrossRefGoogle Scholar
Takács, L. (1955). On stochastic processes generated by a Poisson process and their applications in physics. Acta Math. Hungar. 6, 363–380.CrossRefGoogle Scholar
Vervaat, W. (1979). On a stochastic difference equation and a representation of non–negative infinitely divisible random variables. Anal. Appl. Prob. 11, 750–783.Google Scholar