Hostname: page-component-78c5997874-v9fdk Total loading time: 0 Render date: 2024-11-10T17:01:36.340Z Has data issue: false hasContentIssue false
  • English
  • Français

Extension of Wald's first lemma to Markov processes

Part of: Stochastic processes

Published online by Cambridge University Press:  14 July 2016

George V. Moustakides
George V. Moustakides*
Affiliation:
University of Patras
*
∗Postal address: Department of Computer Engineering and Informatics, University of Patras, 26 500 Patras, Greece. Email address: moustaki@cti.gr.
Get access Rights & Permissions [Opens in a new window]

Abstract

Let ξ0,ξ1,ξ2,… be a homogeneous Markov process and let Sn denote the partial sum Sn = θ(ξ1) + … + θ(ξn), where θ(ξ) is a scalar nonlinearity. If N is a stopping time with 𝔼N < ∞ and the Markov process 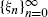satisfies certain ergodicity properties, we then show that 𝔼SN = [limn→∞𝔼θ(ξn)]𝔼N + 𝔼ω(ξ0) − 𝔼ω(ξN). The function ω(ξ) is a well defined scalar nonlinearity directly related to θ(ξ) through a Poisson integral equation, with the characteristic that ω(ξ) becomes zero in the i.i.d. case. Consequently our result constitutes an extension to Wald's first lemma for the case of Markov processes. We also show that, when 𝔼N → ∞, the correction term is negligible as compared to 𝔼N in the sense that 𝔼ω(ξ0) − 𝔼ω(ξN) = o(𝔼N).

Keywords

Wald's lemmastopping times

MSC classification

Primary: 60G40: Stopping times; optimal stopping problems; gambling theory
Type
Research Papers
Information
Journal of Applied Probability , Volume 36 , Issue 1 , March 1999 , pp. 48 - 59
Copyright
Copyright © Applied Probability Trust 1999 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Blackwell, D. (1946). On an equation by Wald. Ann. Math. Statist. 17, 84–87.Google Scholar
Burkholder, D. L., and Gundy, R. F. (1970). Extrapolation and interpolation of quasilinear operators on martingales. Acta Math. 124, 249–304.Google Scholar
Chow, Y. S., Robbins, H., and Siegmund, D. (1971). Great Expectations. The Theory of Optimal Stopping. Houghton Mifflin, New York.Google Scholar
Chow, Y. S., De Le Pena, V. H., and Teicher, H. (1993). Wald's equation for a class of denormalized U-statistics. Ann. Prob. 21, 1151–1158.CrossRefGoogle Scholar
De La Pena, V. H. (1993). Inequalities for tails of adapted processes with an application to Wald's lemma. J. Theoret. Prob. 6, 285–302.Google Scholar
Franken, P., and Lisek, B. (1982). On Wald's identity for dependent variables. Z. Wahrscheinlichkeitsth. 60, 143–150.Google Scholar
Gundy, R. F. (1981). On a theorem of F. and M. Riesz and an equation of A. Wald. Indiana Univ. Math. J. 30, 589–605.Google Scholar
Hoel, P. G., Port, S. C., and Stone, C. J. (1987). Introduction to Stochastic Processes. Waveland Press, Prospect Heights, IL.Google Scholar
Isaacson, D. L., and Madsen, R. W. (1976). Markov Chains Theory and Applications. John Wiley, New York.Google Scholar
Kato, T. (1966). Perturbation Theory for Linear Operators. Springer, New York.Google Scholar
Klass, M. J. (1988). A best possible improvement of Wald's equation. Ann. Prob. 16, 840–853.Google Scholar
Meyn, S. P. and Tweedie, R. L. (1993). Markov Chains and Stochastic Stability. Springer, New York.Google Scholar
Nummelin, E. (1984). General Irreducible Markov Chains and Non-Negative Operators. CUP, Cambridge, UK.Google Scholar
Roters, M. (1994). On the validity of Wald's equation. J. Appl. Prob. 31, 949–957.Google Scholar
Roters, M. (1995). An optimal stopping problem for random walks with non-zero drift. J. Appl. Prob. 32, 956–959.Google Scholar
Sadowsky, J. S. (1989). A dependent data extension of Wald's identity and its application to sequential test performance computation. IEEE Trans. Inform. Theory 35, 834–842.Google Scholar
Shiryayev, A. N. (1978). Optimal Stopping Rules. Springer, New York.Google Scholar
Wald, A. (1945). Sequential tests of statistical hypotheses. Ann. Math. Statist. 16, 117–186.Google Scholar