Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Attia, F. A.
and
Brockwell, P. J.
1982.
The control of a finite dam.
Journal of Applied Probability,
Vol. 19,
Issue. 04,
p.
815.
Attia, F. A.
and
Brockwell, P. J.
1982.
The control of a finite dam.
Journal of Applied Probability,
Vol. 19,
Issue. 4,
p.
815.
Brockwell, Peter J.
1988.
Stochastic models in cell kinetics.
Journal of Applied Probability,
Vol. 25,
Issue. A,
p.
91.
Attia, F. A.
and
Brockwell, P. J.
1993.
On the control of an infinite capacity storage system.
Stochastic Hydrology and Hydraulics,
Vol. 7,
Issue. 3,
p.
195.
Nadarajah, Saralees
2003.
Stochastic Processes: Modelling and Simulation.
Vol. 21,
Issue. ,
p.
607.
Withers, Christopher S.
and
Nadarajah, Saralees
2014.
The distribution and quantiles of the range of a Wiener process.
Applied Mathematics and Computation,
Vol. 232,
Issue. ,
p.
766.

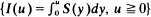 where
where 