Hostname: page-component-cd9895bd7-jkksz Total loading time: 0 Render date: 2024-12-27T09:18:15.998Z Has data issue: false hasContentIssue false
  • English
  • Français

Extremes for shot noise processes with heavy tailed amplitudes

Part of: Markov processes Special processes

Published online by Cambridge University Press:  14 July 2016

William P. McCormick
William P. McCormick*
Affiliation:
University of Georgia
*
∗Postal address: Department of Statistics, University of Georgia, Athens, GA 30602, USA.
Get access Rights & Permissions [Opens in a new window]

Abstract

Extreme value results for a class of shot noise processes with heavy tailed amplitudes are considered. For a process of the form, , where {τ k} are the points of a renewal process and {Ak} are i.i.d. with d.f. having a regularly varying tail, the limiting behavior of the maximum is determined. The extremal index is computed and any value in (0, 1) is possible. 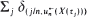Two-dimensional point processes of the form are shown to converge to a compound Poisson point process limit. As a corollary to this result, the joint limiting distribution of high local maxima is obtained.

Keywords

SHOT NOISEEXTREME VALUESRENEWAL PROCESSESWEAK CONVERGENCE

MSC classification

Primary: 60K99: None of the above, but in this section
Secondary: 60K05: Renewal theory 60J05: Discrete-time Markov processes on general state spaces
Type
Research Papers
Information
Journal of Applied Probability , Volume 34 , Issue 3 , September 1997 , pp. 643 - 656
Copyright
Copyright © Applied Probability Trust 1997 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Beirlant, J. and Teugels, J. L. (1992) Modeling large claims in non-life insurance. Insurance: Math. Econ. 11, 17–29.Google Scholar
Bingham, N. H., Goldie, C. H. and Teugels, J. L. (1987) Regular Variation. Cambridge University Press, Cambridge.CrossRefGoogle Scholar
Chernick, M. R., Hsing, T. and McCormick, W. P. (1991) Calculating the extremal index for a class of stationary sequences. Adv. Appl. Prob. 25, 835–850.CrossRefGoogle Scholar
Cline, D. (1983) Infinite series of random variables with regularly varying tails. Tech. report 83-24. University of British Columbia.Google Scholar
Doney, R. A. and O'Brien, G. L. (1991) Loud shot noises. Ann. Appl. Prob. 1, 88–103.CrossRefGoogle Scholar
Holden, H. V. (1976) Models for Stochastic Activity of Neurones (Lecture Notes in Biomathematics 12). Springer, Berlin.CrossRefGoogle Scholar
Homblé, P. and McCormick, W. P. (1995) Weak limit results for the extremes of a class of shot noise processes. J. Appl. Prob. 32, 707–726.Google Scholar
Hsing, T. (1987) On the characterization of certain point processes. Stoch. Proc. Appl. 26, 297–316.CrossRefGoogle Scholar
Hsing, T. (1993) On some estimates based on sample behavior near high level excursions. Prob. Theory Rel. Fields 95, 331–356.CrossRefGoogle Scholar
Hsing, T., Hüsler, J. and Leadbetter, M. R. (1988) On the exceedance point process for stationary sequences. Prob. Theory Rel. Fields 78, 97–112.CrossRefGoogle Scholar
Hsing, T. L. and Teugels, J. L. (1989) Extremal properties of shot noise processes. Adv. Appl. Prob. 21, 513–525.CrossRefGoogle Scholar
Jensen, J. L. (1991) Saddlepoint approximations to the distribution of the total claim amount in some recent risk models. Scand. Act. J 154–168.CrossRefGoogle Scholar
Kallenberg, O. (1976) Random Measures. Academic Press, New York.Google Scholar
Lawrance, A. J. and Kottegoda, H. T. (1977) Stochastic modelling of riverflow time series. J. R. Statist. Soc. A 140, 1–14.Google Scholar
Reiss, R. (1993) A Course on Point Processes. Springer, New York.CrossRefGoogle Scholar
Resnick, S. I. (1987) Extreme Values, Regular Variation, and Point Processes. Springer, New York.CrossRefGoogle Scholar
Resnick, S. I. (1992) Adventures in Stochastic Processes. Birkhäuser, Boston.Google Scholar
Waymire, E. and Gupta, V. K. (1981a) The mathematical structure of rainfall representations 1. A review of the stochastic rainfall models. Water Resources Res. 17, 1261–1272.CrossRefGoogle Scholar
Waymire, E. and Gupta, V. K. (1981b) The mathematical structure of rainfall representations 2. A review of the theory of point processes. Water Resources Res. 17, 1273–1285.CrossRefGoogle Scholar
Waymire, E. and Gupta, V. K. (1981c) The mathematical structure of rainfall representations 3. Some applications of the point process theory to rainfall processes. Water Resources Res. 17, 1287–1294.CrossRefGoogle Scholar
Weiss, G. (1973) Filtered Poisson processes as models for daily streamflow data. PhD thesis. Imperial College, London.Google Scholar
Weiss, G. (1974) Shot noise models for synthetic generation of multisite daily streamflow data. In Design of Water Resource Projects with Inadequate Data. Vol. 1. IAHS. pp. 457–467.Google Scholar