Hostname: page-component-78c5997874-4rdpn Total loading time: 0 Render date: 2024-11-10T16:16:39.581Z Has data issue: false hasContentIssue false
  • English
  • Français

First passage upwards for state-dependent-killed spectrally negative Lévy processes

Part of: Markov processes Stochastic processes

Published online by Cambridge University Press:  30 July 2019

Matija Vidmar
Matija Vidmar*
Affiliation:
University of Ljubljana
*
*Postal address: Department of Mathematics, Faculty of Mathematics and Physics, University of Ljubljana, Jadranska ulica 21, 1000 Ljubljana, Slovenia.
Get access Rights & Permissions [Opens in a new window]

Abstract

For a spectrally negative Lévy process X, killed according to a rate that is a function ω of its position, we complement the recent findings of [12] by analysing (in greater generality) the exit probability of the one-sided upwards passage problem. When ω is strictly positive, this problem is related to the determination of the Laplace transform of the first passage time upwards for X that has been time-changed by the inverse of the additive functional 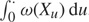$$\int_0^ \cdot \omega ({X_u}){\kern 1pt} {\rm{d}}u$$. In particular, our findings thus shed extra light on related results concerning first passage times downwards (resp. upwards) of continuous-state branching processes (resp. spectrally negative positive self-similar Markov processes).

Keywords

Spectrally negative Lévy processfirst passage upwardskillingtime change

MSC classification

Primary: 60G51: Processes with independent increments; L'evy processes
Secondary: 60J25: Continuous-time Markov processes on general state spaces 60G44: Martingales with continuous parameter
Type
Research Papers
Information
Journal of Applied Probability , Volume 56 , Issue 2 , June 2019 , pp. 472 - 495
Copyright
© Applied Probability Trust 2019 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bertoin, J. (1996). Lévy Processes. Cambridge Tracts in Mathematics. Cambridge University Press.Google Scholar
Carr, P. and WU, L. (2004). Time-changed Lévy processes and option pricing. J. Finan. Econ. 71, 113–141.CrossRefGoogle Scholar
Cissé, M., Patie, P., and Tanré, E. (2012). Optimal stopping problems for some Markov processes. Ann. Appl. Probab. 22, 1243–1265.CrossRefGoogle Scholar
Doney, R. A. (2007). Fluctuation theory for Lévy processes. In Proc. Ecole d’Eté de Probabilités de Saint-Flour XXXV, 2005 ed. Picard, J.. Lecture Notes in Mathematics. Springer, Berlin.Google Scholar
DöRing, L. and Kyprianou, A. E. (2016). Perpetual integrals for Lévy processes. J. Theoret. Prob. 29,1192–1198.CrossRefGoogle Scholar
Duhalde, X., Foucart, C., and MA, C. (2014). On the hitting times of continuous-state branching processes with immigration. Stoch. Process. Appl. 124, 4182–4201.CrossRefGoogle Scholar
Getoor, R.K. And Blumenthal, R. M. (2011). Markov Processes and Potential Theory. Pure and Applied Mathematics. Elsevier Science, New York.Google Scholar
Khoshnevisan, D., Salminen, P., and YOR, M. (2006). A note on a.s. finiteness of perpetual integral functionals of diffusions. Electron. Commun. Prob. 11, 108–117.CrossRefGoogle Scholar
Klingler, S., Kim, Y.S., Rachev, S.T., and Fabozzi, F. J. (2013). Option pricing with time-changed Lévy processes. Appl, Finan. Econ. 23, 1231–1238.CrossRefGoogle Scholar
Kuznetsov, A., Kyprianou, A.E., and Rivero, V. (2013). The theory of scale functions for spectrally negative Lévy processes. In Lévy Matters II: Recent Progress in Theory and Applications: Fractional Lévy Fields, and Scale Functions. Springer, Berlin, pp. 97–186.Google Scholar
Kyprianou, A. E. (2014). Fluctuations of Lévy Processes with Applications: Introductory Lectures. Springer-Verlag, Berlin.CrossRefGoogle Scholar
Li, B. and Palmowski, Z. (2018). Fluctuations of Omega-killed spectrally negative Lévy processes. Stoch. Process. Appl. 128, 3273–3299.CrossRefGoogle Scholar
Long, M. and Zhang, H. (2018 (to appear)). On the optimality of threshold type strategies in single and recursive optimal stopping under Lévy models. To appear in Stoch. Process. Appl.Google Scholar
Patie, P. (2009). Infinite divisibility of solutions to some self-similar integro-differential equations and exponential functionals of Lévy processes. Annales de l’Institut Henri Poincaré, Prob. Stat. 45, 667–684.Google Scholar
Pitman, J. and YOR, M. (1981). Bessel processes and infinitely divisible laws. In Stochastic Integrals. ed. Williams, D.. Vol. 851 of Lecture Notes in Mathematics. Springer, Berlin, pp. 285–370.Google Scholar
Revuz, D. and YOR, M. (2004). Continuous Martingales and Brownian Motion. Grundlehren der mathematischen Wissenschaften. Springer, Berlin.Google Scholar
Rodosthenous, N. and Zhang, H. (2018). Beating the omega clock: An optimal stopping problem with random time-horizon under spectrally negative Lévy models. Ann. Appl. Prob. 28, 2105–2140.CrossRefGoogle Scholar
Sato, K.I. (1999). Lévy Processes and Infinitely Divisible Distributions. Cambridge studies in advanced mathematics. Cambridge University Press.Google Scholar
Tankov, P. (2011). Pricing and hedging in exponential Lévy models: Review of recent results. In Paris– Princeton Lectures on Mathematical Finance 2010. Springer, Berlin, pp. 319–359.CrossRefGoogle Scholar
Vidmar, M. (2018). Exit problems for positive self-similar Markov processes with one-sided jumps. Preprint, arXiv:1807.00486v2.Google Scholar
Yeh, J. (2006). Real Analysis: Theory of Measure and Integration. World Scientific, Singapore.CrossRefGoogle Scholar