Hostname: page-component-78c5997874-v9fdk Total loading time: 0 Render date: 2024-11-10T19:23:52.635Z Has data issue: false hasContentIssue false
  • English
  • Français

A gaussian process with parabolic covariances

Published online by Cambridge University Press:  14 July 2016

Enrique M. Cabaña
Enrique M. Cabaña*
Affiliation:
Universidad de la República
*
∗ Postal address: Centro de Matemática, Facultad de Ciencias Exactas y Naturales, Universidad de la República, Montevideo, Uruguay.
Get access Rights & Permissions [Opens in a new window]

Abstract

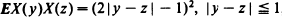The centred, periodic, stationary Gaussian process X(z), ≧ z ≧ 1 with covariances , appears when one studies the solutions of the vibrating string equation forced by noise, corresponding to the case of a finite string with the extremes tied together. The close relationship between this process and a Brownian bridge permits us to compute the distribution of the maximum excursion of the string at particular times.

Keywords

PERIODIC GAUSSIAN PROCESSPARABOLIC COVARIANCEBROWNIAN BRIDGE
Type
Short Communications
Information
Journal of Applied Probability , Volume 28 , Issue 4 , December 1991 , pp. 898 - 902
Copyright
Copyright © Applied Probability Trust 1991 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1] Cabaña, E. M. (1970) The vibrating string forced by white noise. Z. Wahrscheinlichkeitsth. 15, 111–130.Google Scholar
[2] Cabaña, A. and Cabaña, E. M. (1991) Strong Markov property for the vibrating string forced by white noise. Submitted.Google Scholar
[3] Freedman, D. (1983) Brownian Motion and Diffusion. Springer-Verlag, Berlin.10.1007/978-1-4615-6574-1Google Scholar
[4] Knight, F. B. (1981) Essentials of Brownian Motion and Diffusion. Mathematical Surveys 18, American Mathematical Society, Providence, RI.Google Scholar
[5] Walsh, J. B. (1986) An introduction to stochastic partial differential equations. In Lecture Notes in Mathematics 1180, pp. 256–437. Springer-Verlag, Berlin.Google Scholar