Hostname: page-component-78c5997874-t5tsf Total loading time: 0 Render date: 2024-11-10T17:44:15.519Z Has data issue: false hasContentIssue false
  • English
  • Français

Generalized limit theorems for U-max statistics

Part of: Geometric probability and stochastic geometry Stochastic processes Limit theorems

Published online by Cambridge University Press:  11 July 2022

Yakov Nikitin  and
Ekaterina Simarova Open the ORCID record for Ekaterina Simarova [Opens in a new window]
Yakov Nikitin*
Affiliation:
Saint-Petersburg State University
Ekaterina Simarova*
Affiliation:
Saint-Petersburg State University and Leonhard Euler International Mathematical Institute
*
*Postal address: Department of Mathematics and Mechanics, Universitetsky pr. 28, Stary Peterhof 198504, Russia.
*Postal address: Department of Mathematics and Mechanics, Universitetsky pr. 28, Stary Peterhof 198504, Russia.
Get access Rights & Permissions [Opens in a new window]

Abstract

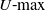$U{\hbox{-}}\textrm{max}$ statistics were introduced by Lao and Mayer in 2008. Such statistics are natural in stochastic geometry. Examples are the maximal perimeters and areas of polygons and polyhedra formed by random points on a circle, ellipse, etc. The main method to study limit theorems for 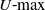$U{\hbox{-}}\textrm{max}$ statistics is via a Poisson approximation. In this paper we consider a general class of kernels defined on a circle, and we prove a universal limit theorem with the Weibull distribution as a limit. Its parameters depend on the degree of the kernel, the structure of its points of maximum, and the Hessians of the kernel at these points. Almost all limit theorems known so far may be obtained as simple special cases of our general theorem. We also consider several new examples. Moreover, we consider not only the uniform distribution of points but also almost arbitrary distribution on a circle satisfying mild additional conditions.

Keywords

Weibull distributionPoisson approximationU-max statisticsrandom perimeterrandom area

MSC classification

Primary: 60D05: Geometric probability and stochastic geometry
Secondary: 60F05: Central limit and other weak theorems 60G70: Extreme value theory; extremal processes
Type
Original Article
Information
Journal of Applied Probability , Volume 59 , Issue 3 , September 2022 , pp. 825 - 848
Check for updates
Copyright
© The Author(s), 2022. Published by Cambridge University Press on behalf of Applied Probability Trust

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Alexander, R. and Stolarsky, K. B. (1974). Extremal problems of distance geometry related to energy integrals. Trans. Amer. Math. Soc. 193, 1–31.10.1090/S0002-9947-1974-0350629-3CrossRefGoogle Scholar
Barbour, A. D., Holst, L. and Janson, S. (1992). Poisson Approximation. Oxford University Press, London.Google Scholar
Halmos, P. (1946). The theory of unbiased estimation. Ann. Math. Statist. 17, 34–43.10.1214/aoms/1177731020CrossRefGoogle Scholar
Hoeffding, W. (1948). A class of statistics with asymptotically normal distribution. Ann. Math. Statist. 19, 293–325.10.1214/aoms/1177730196CrossRefGoogle Scholar
Horn, R. A. and Johnson, C. R. (2012). Matrix Analysis. Cambridge University Press.10.1017/CBO9781139020411CrossRefGoogle Scholar
Koroleva, E. V. and Nikitin, Ya. Yu. (2014). U-max-statistics and limit theorems for perimeters and areas of random polygons. J. Multivariate Anal. 127, 98–111.10.1016/j.jmva.2014.02.006CrossRefGoogle Scholar
Korolyuk, V. S. and Borovskikh, V., Y. (1994). Theory of U-Statistics. Springer, Dordrecht.10.1007/978-94-017-3515-5CrossRefGoogle Scholar
Kurzhanski, A. and Valyi, I. (1997). Ellipsoidal Calculus for Estimation and Control. Birkhäuser, Basel; Springer Science and Business Media, New York.10.1007/978-1-4612-0277-6CrossRefGoogle Scholar
Lao, W. (2010). Some weak limit laws for the diameter of random point sets in bounded regions. Doctoral thesis, Karlsruhe Institute of Technology.Google Scholar
Lao, W. and Mayer, M. (2008). U-max-statistics. J. Multivariate Anal. 99, 2039–2052.10.1016/j.jmva.2008.02.001CrossRefGoogle Scholar
Lee, A. J. (2019). U-Statistics: Theory and Practice. Routledge.10.1201/9780203734520CrossRefGoogle Scholar
Makarov, B. and Podkorytov, A. (2013). Real Analysis: Measures, Integrals and Applications. Springer, London.10.1007/978-1-4471-5122-7CrossRefGoogle Scholar
Mardia, K. V. and Jupp, P. E. (2000). Directional Statistics. Wiley.Google Scholar
Mayer, M. (2008). Random diameters and other U-max-statistics. Doctoral thesis, University of Bern.Google Scholar
Polevaya, T. A. and Nikitin, Ya. Yu (2019). Limit theorems for areas and perimeters of random inscribed and circumscribed polygons. Zap. Nauchn. Sem. POMI 486, 200–213 (in Russian).Google Scholar
Silverman, F. and Brown, T. (1978). Short distances, flat triangles, and Poisson limits. J. Appl. Prob. 15, 815–825.10.2307/3213436CrossRefGoogle Scholar
Simarova, E. N. (2020). Limit theorems for generalized perimeters of random inscribed polygons I. Vestnik St. Petersburg Univ. Math. Mech. Astronom. 7, 678–687 (in Russian). English translation: Vestnik St. Petersburg Univ. Math. 53, 434–442.10.1134/S1063454120040093CrossRefGoogle Scholar
Simarova, E. N. (2021). Limit theorems for generalized perimeters of random inscribed polygons II. Vestnik St. Petersburg Univ. Math. Mech. Astronom. 8, 101–110 (in Russian). English translation: Vestnik St. Petersburg Univ. Math. 54, 78–85.10.1134/S1063454121010106CrossRefGoogle Scholar
Toth, L. F. (1956). On the sum of distances determined by a pointset. Acta Math. Hungar. 7, 397–401.10.1007/BF02020534CrossRefGoogle Scholar
Yaglom, I. M. and Boltyanskii, V. (1961). Convex Figures. Holt, Rinehart and Winston, New York.Google Scholar
Zorich, V. A. (2015). Mathematical Analysis I. Springer, Berlin and Heidelberg.10.1007/978-3-662-48792-1CrossRefGoogle Scholar