Hostname: page-component-6bf8c574d5-vmclg Total loading time: 0 Render date: 2025-02-22T18:08:19.925Z Has data issue: false hasContentIssue false
  • English
  • Français

Giant descendant trees, matchings, and independent sets in age-biased attachment graphs

Part of: Graph theory Combinatorial probability

Published online by Cambridge University Press:  25 April 2022

Hüseyin Acan Open the ORCID record for Hüseyin Acan [Opens in a new window] ,
Alan Frieze  and
Boris Pittel
Hüseyin Acan*
Affiliation:
Drexel University
Alan Frieze*
Affiliation:
Carnegie Mellon University
Boris Pittel*
Affiliation:
Ohio State University
*
*Postal address: Department of Mathematics, Drexel University, Philadelphia, PA 19104, USA. Email: huseyin.acan@drexel.edu
**Postal address: Department of Mathematical Sciences, Carnegie Mellon University, Pittsburgh, PA 15213, USA. Email: alan@random.math.cmu.edu
***Postal address: Department of Mathematics, Ohio State University, Columbus, OH 43210, USA. Email: bgp@math.ohio-state.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

We study two models of an age-biased graph process: the 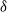$\delta$ -version of the preferential attachment graph model (PAM) and the uniform attachment graph model (UAM), with m attachments for each of the incoming vertices. We show that almost surely the scaled size of a breadth-first (descendant) tree rooted at a fixed vertex converges, for 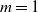$m=1$ , to a limit whose distribution is a mixture of two beta distributions and a single beta distribution respectively, and that for 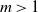$m>1$ the limit is 1. We also analyze the likely performance of two greedy (online) algorithms, for a large matching set and a large independent set, and determine – for each model and each greedy algorithm – both a limiting fraction of vertices involved and an almost sure convergence rate.

Keywords

Randompreferential attachment graphasymptotics

MSC classification

Primary: 05C80: Random graphs
Secondary: 05C05: Trees 60C05: Combinatorial probability 05C30: Enumeration in graph theory
Type
Original Article
Information
Journal of Applied Probability , Volume 59 , Issue 2 , June 2022 , pp. 299 - 324
Check for updates
Copyright
© The Author(s), 2022. Published by Cambridge University Press on behalf of Applied Probability Trust

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Acan, H. and Hitczenko, P. (2016). On a memory game and preferential attachment graphs. Adv. Appl. Prob. 48, 585–609.CrossRefGoogle Scholar
Acan, H. and Pittel, B. (2019). On connectivity, conductance and bootstrap percolation for the uniformly random k-out, age-biased graph. Random Structures Algorithms 56, 37–62.CrossRefGoogle Scholar
Barabási, I. and Albert, R. (1999). Emergence of scaling in random networks. Science 286, 509–512.CrossRefGoogle ScholarPubMed
Berger, N., Borgs, C., Chayes, J. T. and Saberi, A. (2014). Asymptotic behavior and distributional limits of preferential attachment graphs. Ann. Prob. 42, 1–40.CrossRefGoogle Scholar
Bollobás, B. (2001). Random Graphs, 2nd edn. Cambridge University Press.CrossRefGoogle Scholar
Bollobás, B. and Riordan, O. (2000). Linearized chord diagrams and an upper bound for the Vassiliev invariants. J. Knot Theory Ramifications 9, 847–853.CrossRefGoogle Scholar
Bollobás, B. and Riordan, O. (2002). Mathematical results on scale-free random graphs. In Handbook of Graphs and Networks: From the Genome to the Internet, eds S. Bornholdt and H. G. Schuster, pp. 1–34. Wiley-VCH.CrossRefGoogle Scholar
Bollobás, B. and Riordan, O. (2003). Robustness and vulnerability of scale-free random graphs. Internet Math. 1, 1–35.CrossRefGoogle Scholar
Bollobás, B. and Riordan, O. (2004). The diameter of a scale-free random graph. Combinatorica 4, 5–34.CrossRefGoogle Scholar
Bollobás, B., Borgs, C., Chayes, J. and Riordan, O. (2003). Directed scale-free graphs. In Proceedings of the 14th Annual ACM–SIAM SODA Conference, pp. 132–139. ACM Press.Google Scholar
Bollobás, B., Riordan, O., Spencer, J. and Tusnády, G. (2001). The degree sequence of a scale-free random graph process. Random Structures Algorithms 18, 279–290.CrossRefGoogle Scholar
Borgs, C., Brautbar, M., Chayes, J., Khanna, S. and Lucier, B. (2012). The power of local information in social networks. In International Workshop on Internet and Network Economics WINE 2012: Internet and Network Economics (Lecture Notes Comput. Sci. 7695), pp. 406–419. Springer, Berlin and Heidelberg.CrossRefGoogle Scholar
Comtet, L. (1974). Advanced Combinatorics. D. Reidel, Dordrecht.CrossRefGoogle Scholar
Cooper, C. and Frieze, A. M. (2003). Crawling on web graphs. Internet Math. 1, 57–90.CrossRefGoogle Scholar
Cooper, C. and Frieze, A. M. (2007). The cover time of the preferential attachment graph. J. Combinatorial Theory B 97, 269–290.CrossRefGoogle Scholar
Cooper, C., Klasing, R. and Zito, M. (2005). Lower bounds and algorithms for dominating sets in web graphs. Internet Math. 2, 275–300.CrossRefGoogle Scholar
Erdős, P. and Rényi, A. (1959). On random graphs I. Publ. Math. Debrecen 6, 290–297.Google Scholar
Flaxman, A., Frieze, A. M. and Fenner, T. (2005). High degree vertices and eigenvalues in the preferential attachment graph. Internet Math. 2, 1–20.CrossRefGoogle Scholar
Frieze, A. M. and Karoński, M. (2016). Introduction to Random Graphs. Cambridge University Press.Google Scholar
Frieze, A. M. and Pegden, W. (2017). Looking for vertex number one. Ann. Appl. Prob. 27, 582–630.CrossRefGoogle Scholar
Frieze, A. M., Pérez-Giménez, X., Prałat, P. and Reiniger, B. (2019). Perfect matchings and Hamiltonian cycles in the preferential attachment model. Random Structures Algorithms 54, 258–288.CrossRefGoogle Scholar
Gilbert, E. N. (1959). Random graphs. Ann. Math. Statist. 30, 1141–1144.CrossRefGoogle Scholar
van der Hofstad, R. (2017). Random Graphs and Complex Networks, Vol. 1. Cambridge University Press.Google Scholar
Janson, S. (2019). Random recursive trees and preferential attachment trees are random split trees. Combinatorics Prob. Comput. 28, 81–99.CrossRefGoogle Scholar
Janson, S. and Warnke, L. (2021). Preferential attachment without vertex growth: emergence of the giant component. Ann. Appl. Prob. 31, 1523–1547.CrossRefGoogle Scholar
Janson, S., Łuczak, T. and Ruciński, A. (2000). Random Graphs. Wiley, New York.CrossRefGoogle Scholar
Katona, Z. and Móri, T. (2006). A new class of scale free random graphs. Statist. Prob. Lett. 76, 1587–1593.CrossRefGoogle Scholar
Mihail, M., Papadimitriou, C. and Saberi, A. (2006). On certain connectivity properties of the internet topology. J. Comput. System Sci. 72, 239–251.CrossRefGoogle Scholar
Molloy, M. (1998). The probabilistic method. In Probabilistic Methods for Algorithmic Discrete Mathematics (Algorithms and Combinatorics 16), pp. 1–35. Springer, Berlin and Heidelberg.CrossRefGoogle Scholar
Móri, T. (2003). On random trees. Studia Sci. Math. Hungar. 39, 143–155.Google Scholar
Móri, T. (2005). The maximum degree of the Barabási–Albert random tree. Combinatorics Prob. Comput. 14, 339–348.CrossRefGoogle Scholar
Peköz, E., Röllin, A. and Ross, N. (2017). Joint degree distributions of preferential attachment random graphs. Adv. Appl. Prob. 49, 368–387.CrossRefGoogle Scholar
Pittel, B. (1982). On the probable behaviour of some algorithms for finding the stability number of a graph. Math. Proc. Camb. Phil. Soc. 92, 511–526.CrossRefGoogle Scholar
Pittel, B. (1994). Note on the heights of random recursive trees and random m-ary search trees. Random Structures Algorithms 5, 337–347.CrossRefGoogle Scholar
Pittel, B. (2010). On a random graph evolving by degrees. Adv. Math. 223, 619–671.CrossRefGoogle Scholar
Pittel, B. (2021) On Bollobás–Riordan random pairing model of preferential attachment graph. Random Structures Algorithms 58, 691–725.CrossRefGoogle Scholar
Talagrand, M. (1995) Concentration of measure and isoperimetric inequalities in product spaces. Institut des Hautes Études Scientifiques, Publications Mathématiques 81, 73–205.CrossRefGoogle Scholar