Hostname: page-component-cd9895bd7-jkksz Total loading time: 0 Render date: 2024-12-26T19:36:53.613Z Has data issue: false hasContentIssue false
  • English
  • Français

Improvements on the distribution of maximal segmental scores in a Markovian sequence

Part of: Limit theorems Special processes Markov processes Stochastic processes

Published online by Cambridge University Press:  04 May 2020

S. Grusea  and
S. Mercier
S. Grusea*
Affiliation:
Institut de Mathématiques de Toulouse
S. Mercier*
Affiliation:
Institut de Mathématiques de Toulouse
*
*Postal address: Institut National des Sciences Appliquées, 135 avenue de Rangueil, 31400, Toulouse, France.
***Postal address: Institut de Mathématiques de Toulouse, UMR5219, Université de Toulouse 2 Jean Jaurès, 5 allées Antonio Machado, 31058, Toulouse, Cedex 09, France.
Get access Rights & Permissions [Opens in a new window]

Abstract

Let 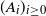$(A_i)_{i \geq 0}$ be a finite-state irreducible aperiodic Markov chain and f a lattice score function such that the average score is negative and positive scores are possible. Define 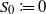$S_0\coloneqq 0$ and 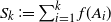$S_k\coloneqq \sum_{i=1}^k f(A_i)$ the successive partial sums, 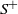$S^+$ the maximal non-negative partial sum, 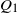$Q_1$ the maximal segmental score of the first excursion above 0, and 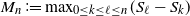$M_n\coloneqq \max_{0\leq k\leq\ell\leq n} (S_{\ell}-S_k)$ the local score, first defined by Karlin and Altschul (1990). We establish recursive formulae for the exact distribution of 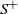$S^+$ and derive a new approximation for the tail behaviour of 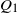$Q_1$ , together with an asymptotic equivalence for the distribution of 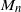$M_n$ . Computational methods are explicitly presented in a simple application case. The new approximations are compared with those proposed by Karlin and Dembo (1992) in order to evaluate improvements, both in the simple application case and on the real data examples considered by Karlin and Altschul (1990).

Keywords

local scoreMarkov theorylimit theoremsmaximal segmental score

MSC classification

Primary: 60J10: Markov chains (discrete-time Markov processes on discrete state spaces) 60F05: Central limit and other weak theorems 60G70: Extreme value theory; extremal processes
Secondary: 60F10: Large deviations 60K15: Markov renewal processes, semi-Markov processes
Type
Research Papers
Information
Journal of Applied Probability , Volume 57 , Issue 1 , March 2020 , pp. 29 - 52
Copyright
© Applied Probability Trust 2020

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Athreya, K. B. and Rama Murthy, K. (1976). Feller’s renewal theorem for systems of renewal equations. J. Indian Inst. 58, 437–459.Google Scholar
Cellier, D., Charlot, F. and Mercier, S. (2003). An improved approximation for assessing the statistical of molecular sequence features. J. Appl. Prob., 40, 427–441.Google Scholar
Dembo, A. and Karlin, S. (1991). Strong limit theorems of empirical distributions for large segmental exceedances of partial sums of Markov variables. Ann. Prob., 19, 1756–1767.CrossRefGoogle Scholar
Durbin, R., Eddy, S., and Krogh, A. and Mitchion, G. (1998). Biological Sequence Analysis: Probabilistic Models of Proteins and Nucleic Acids. Cambridge University Press.CrossRefGoogle Scholar
Fariello, M.-I.et al. (2017). A new local score based method applied to behavior-divergent quail lines sequenced in pools precisely detects selection signatures on genes related to autism. Molec. Ecol. 26, 3700–3714.CrossRefGoogle Scholar
Guedj, M.et al. (2006). Detecting local high-scoring segments: a first-stage approach for genome-wide association studies. Statist. Appl. Genet. Mol. Biol., 5, 22.CrossRefGoogle ScholarPubMed
Hassenforder, C. and Mercier, S. (2007). Exact distribution of the local score for Markovian sequences. Ann. Inst. Statist. Math., 59, 741–755.CrossRefGoogle Scholar
Karlin, S. and Altschul, S.-F. (1990). Methods for assessing the statistical significance of molecular sequence features by using general scoring schemes. Proc. Nat. Acad. Sci. USA, 87, 2264–2268.CrossRefGoogle ScholarPubMed
Karlin, S. and Dembo, A. (1992). Limit distributions of maximal segmental score among Markov-dependent partial sums. Adv. Appl. Prob., 24, 113–140.CrossRefGoogle Scholar
Karlin, S. and Ost, F. (1987). Counts of long aligned word matches among random letter sequences. Adv. Appl. Prob., 19, 293–351.CrossRefGoogle Scholar
Lancaster, P. (1969). Theory of Matrices. Academic Press, New York.Google Scholar
Mercier, S. and Daudin, J. J. (2001). Exact distribution for the local score of one i.i.d. random sequence. J. Comput. Biol., 8, 373–380.CrossRefGoogle ScholarPubMed