Hostname: page-component-6bf8c574d5-rwnhh Total loading time: 0 Render date: 2025-02-27T23:31:59.664Z Has data issue: false hasContentIssue false
  • English
  • Français

Large deviations of extremal eigenvalues of sample covariance matrices

Part of: Limit theorems Basic linear algebra Probability theory on algebraic and topological structures

Published online by Cambridge University Press:  24 April 2023

Denise Uwamariya  and
Xiangfeng Yang
Denise Uwamariya*
Affiliation:
Linköping University
Xiangfeng Yang*
Affiliation:
Linköping University
*
*Postal address: Department of Mathematics, Linköping University, SE-581 83 Linköping, Sweden.
*Postal address: Department of Mathematics, Linköping University, SE-581 83 Linköping, Sweden.
Get access Rights & Permissions [Opens in a new window]

Abstract

Large deviations of the largest and smallest eigenvalues of 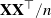$\mathbf{X}\mathbf{X}^\top/n$ are studied in this note, where 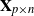$\mathbf{X}_{p\times n}$ is a 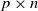$p\times n$ random matrix with independent and identically distributed (i.i.d.) sub-Gaussian entries. The assumption imposed on the dimension size p and the sample size n is 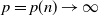$p=p(n)\rightarrow\infty$ with 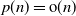$p(n)={\mathrm{o}}(n)$. This study generalizes one result obtained in [3].

Keywords

Large deviationssample covariance matricesextremal eigenvalues

MSC classification

Primary: 60B20: Random matrices (probabilistic aspects; for algebraic aspects see )
Secondary: 60F10: Large deviations 15A12: Conditioning of matrices
Type
Original Article
Information
Journal of Applied Probability , Volume 60 , Issue 4 , December 2023 , pp. 1275 - 1280
Check for updates
Copyright
© The Author(s), 2023. Published by Cambridge University Press on behalf of Applied Probability Trust

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bai, Z. and Yin, Y. (1993). Limit of the smallest eigenvalue of a large dimensional sample covariance matrix. Ann. Prob. 21, 1275–1294.CrossRefGoogle Scholar
Dembo, A. and Zeitouni, O. (2010). Large Deviations Techniques and Applications, corrected reprint of 2nd (1998) edn. Springer, Berlin.Google Scholar
Fey, A., van der Hofstad, R. and Klok, M. (2008). Large deviations for eigenvalues of sample covariance matrices, with applications to mobile communication systems. Adv. Appl. Prob. 40, 1048–1071.CrossRefGoogle Scholar
Jiang, T. and Li, D. (2015). Approximation of rectangular beta-Laguerre ensembles and large deviations. J. Theoret. Prob. 28, 804–847.CrossRefGoogle Scholar
Johansson, K. (2000). Shape fluctuations and random matrices. Commun. Math. Phys. 209, 437–476.CrossRefGoogle Scholar
Johnstone, I. (2001). On the distribution of the largest eigenvalue in principal components analysis. Ann. Statist. 29, 295–327.CrossRefGoogle Scholar
Rogers, C. (1963). Covering a sphere with spheres. Mathematika 10, 157–164.CrossRefGoogle Scholar
Roy, S. (1953). On a heuristic method of test construction and its use in multivariate analysis. Ann. Math. Statist. 24, 220–238.CrossRefGoogle Scholar
Singull, M., Uwamariya, D. and Yang, X. (2021). Large-deviation asymptotics of condition numbers of random matrices. J. Appl. Prob. 58, 1114–1130.CrossRefGoogle Scholar
Vershynin, R. (2012). Introduction to the non-asymptotic analysis of random matrices. In Compressed Sensing: Theory and Applications, ed. Y. Eldar and G. Kutyniok, pp. 210–268. Cambridge University Press, Cambridge.Google Scholar
Yin, Y. Q., Bai, Z. D. and Krishnaiah, P. (1988). On the limit of the largest eigenvalue of the large dimensional sample covariance matrix. Prob. Theory Relat. Fields 78, 509–521.CrossRefGoogle Scholar