Hostname: page-component-745bb68f8f-mzp66 Total loading time: 0 Render date: 2025-01-14T17:39:35.106Z Has data issue: false hasContentIssue false
  • English
  • Français

Large deviations of heavy-tailed random sums with applications in insurance and finance

Part of: Stochastic processes Special processes Limit theorems Applications

Published online by Cambridge University Press:  14 July 2016

C. Klüppelberg  and
T. Mikosch
C. Klüppelberg*
Affiliation:
Johannes Gutenberg University Mainz
T. Mikosch*
Affiliation:
University of Groningen
*
∗Postal address: Department of Mathematics, Johannes Gutenberg University Mainz, D-55099 Mainz, Germany.
∗∗Postal address: Department of Mathematics, University of Groningen, P.O. Box 800, NL-9700 Groningen, The Netherlands.
Get access Rights & Permissions [Opens in a new window]

Abstract

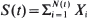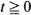We prove large deviation results for the random sum , , where 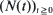are non-negative integer-valued random variables and are 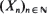i.i.d. non-negative random variables with common distribution function 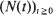F, independent of . Special attention is paid to the compound Poisson process and its ramifications. The right tail of the distribution function F is supposed to be of Pareto type (regularly or extended regularly varying). The large deviation results are applied to certain problems in insurance and finance which are related to large claims.

Keywords

COMPOUND POISSON PROCESSEXTREME VALUE THEORYFINANCIAL RISKFUTURESHIGH DENSITY DATAINSURANCE RISKLARGE DEVIATIONSREGULAR VARIATIONREINSURANCERENEWAL COUNTING PROCESSSUBEXPONENTIAL DISTRIBUTIONS

MSC classification

Primary: 60F10: Large deviations 60F05: Central limit and other weak theorems 60G50: Sums of independent random variables; random walks
Secondary: 60K10: Applications (reliability, demand theory, etc.) 62P05: Applications to actuarial sciences and financial mathematics
Type
Research Article
Information
Journal of Applied Probability , Volume 34 , Issue 2 , June 1997 , pp. 293 - 308
Copyright
Copyright © Applied Probability Trust 1997 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Aase, K. (1994) An equilibrium model of catastrophic insurance futures contracts. Preprint. Google Scholar
Albrecht, P., König, A. and Schradin, H. R. (1994) Katastrophenversicherungs-Termingeschäfte: Grundlagen und Anwendungen im Risikomanagement von Versicherungsunternehmen. Mannheimer Manuskripte zur Versicherungsbetriebslehre, Finanzmanagement und Risikotheorie. No. 72. Universität Mannheim.Google Scholar
Athreya, K. B. and Ney, P. E. (1972) Branching Processes. Springer, Berlin.CrossRefGoogle Scholar
Bingham, N. H., Goldie, C. M. and Teugels, J. L. (1987) Regular Variation. Cambridge University Press, Cambridge.CrossRefGoogle Scholar
Chicago Board Of Trade (Cbot) (1992) Homeowners futures and hedging insurance price risk.Google Scholar
Cistyakov, V. P. (1964) A theorem on the sums of independent positive random variables and its applications to branching random processes. Theory Prob. Appl. 9, 640–648.CrossRefGoogle Scholar
Cline, D. B. and Hsing, T. (1991) Large deviation probabilities for sums and maxima of random variables with heavy or subexponential tails. Preprint. Texas A & M University.Google Scholar
Cummins, J. D. and Geman, H. (1994) An Asian option approach to the valuation of insurance futures contracts. Rev. Futures Markets 13, 517–557.Google Scholar
Embrechts, P., Goldie, C. M. and Veraverbere, N. (1979) Subexponentiality and infinite divisibility. Z. Wahrscheinlichkeitsth. 49, 335–347.CrossRefGoogle Scholar
Embrechts, P., Klüppelberg, C. and Mikosch, T. (1997) Modelling Extremal Events for Insurance and Finance. Springer, Berlin.CrossRefGoogle Scholar
Embrechts, P. and Veraverbere, N. (1982) Estimates for the probability of ruin with special emphasis on the possibility of large claims. Ins. Math. Econ. 1, 55–72.CrossRefGoogle Scholar
Gut, A. (1988) Stopped Random Walk. Limit Theorems and Applications. Springer, New York.CrossRefGoogle Scholar
Heyde, C. C. (1967a) A contribution to the theory of large deviations for sums of independent random variables. Z. Wahrscheinlichkeitsth. 7, 303–308.CrossRefGoogle Scholar
Heyde, C. C. (1967b) On large deviation problems for sums of random variables which are not attracted to the normal law. Ann. Math. Statist. 38, 1575–1578.CrossRefGoogle Scholar
Heyde, C. C. (1968) On large deviation probabilities in the case of attraction to a nonnormal stable law. Sankhya 30, 253–258.Google Scholar
Meister, S. (1995) Contributions to the mathematics of catastrophe insurance futures. Diplomarbeit. ?TH, Zürich.Google Scholar
Nagaev, A. V. (1969a) Integral limit theorems for large deviations when Cramér's condition is not fulfilled I, II. Theory Prob. Appl. 14, 51–64, 193-208.CrossRefGoogle Scholar
Nagaev, A. V. (1969b) Limit theorems for large deviations when Cramér's conditions are violated. (In Russian.) Fiz-Mat. Nauk. 7, 17–22.Google Scholar
Nagaev, S. V. (1973) Large deviations for sums of independent random variables. In Trans. Sixth Prague Conf. on Information Theory, Random Processes and Statistical Decision Functions. Academia, Prague. pp. 657–674.Google Scholar
Nagaev, S. V. (1979) Large deviations of sums of independent random variables. Ann. Prob. 7, 745–789.CrossRefGoogle Scholar
Pakes, A. G. (1975) On the tails of waiting-time distributions. J. Appl. Prob. 12, 555–564.CrossRefGoogle Scholar
Petrov, V. V. (1975) Sums of Independent Random Variables. Springer, Berlin.Google Scholar
Pinelis, I. F. (1985) On the asymptotic equivalence of probabilities of large deviations for sums and maxima of independent random variables. (In Russian.) In Limit Theorems in Probability Theory. (Trudy Inst. Math. 5.) Nauka, Novosibirsk.Google Scholar