Hostname: page-component-cd9895bd7-gbm5v Total loading time: 0 Render date: 2024-12-28T00:54:24.806Z Has data issue: false hasContentIssue false
  • English
  • Français

Large-deviation asymptotics of condition numbers of random matrices

Part of: Basic linear algebra Limit theorems Probability theory on algebraic and topological structures

Published online by Cambridge University Press:  22 November 2021

Martin Singull ,
Denise Uwamariya  and
Xiangfeng Yang
Martin Singull*
Affiliation:
Linköping University
Denise Uwamariya*
Affiliation:
Linköping University
Xiangfeng Yang*
Affiliation:
Linköping University
*
*Postal address: Department of Mathematics, Linköping University, SE-581 83 Linköping, Sweden.
*Postal address: Department of Mathematics, Linköping University, SE-581 83 Linköping, Sweden.
*Postal address: Department of Mathematics, Linköping University, SE-581 83 Linköping, Sweden.
Get access Rights & Permissions [Opens in a new window]

Abstract

Let 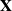$\mathbf{X}$ be a 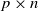$p\times n$ random matrix whose entries are independent and identically distributed real random variables with zero mean and unit variance. We study the limiting behaviors of the 2-normal condition number k(p,n) of 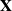$\mathbf{X}$ in terms of large deviations for large n, with p being fixed or 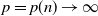$p=p(n)\rightarrow\infty$ with 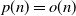$p(n)=o(n)$ . We propose two main ingredients: (i) to relate the large-deviation probabilities of k(p,n) to those involving n independent and identically distributed random variables, which enables us to consider a quite general distribution of the entries (namely the sub-Gaussian distribution), and (ii) to control, for standard normal entries, the upper tail of k(p,n) using the upper tails of ratios of two independent 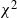$\chi^2$ random variables, which enables us to establish an application in statistical inference.

Keywords

Condition numberslarge deviationsrandom matricesWishart matrices

MSC classification

Primary: 60B20: Random matrices (probabilistic aspects; for algebraic aspects see )
Secondary: 60F10: Large deviations 15A12: Conditioning of matrices
Type
Original Article
Information
Journal of Applied Probability , Volume 58 , Issue 4 , December 2021 , pp. 1114 - 1130
Check for updates
Copyright
© The Author(s), 2021. Published by Cambridge University Press on behalf of Applied Probability Trust

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Anderson, W. and Wells, M. (2009). The exact distribution of the condition number of a Gaussian matrix. SIAM J. Matrix Anal. Appl. 31, 1125–1130.10.1137/070698932CrossRefGoogle Scholar
Bai, Z., Silverstein, J. and Yin, Y. (1988). A note on the largest eigenvalue of a large-dimensional sample covariance matrix. J. Multivar. Anal. 26, 166–168.10.1016/0047-259X(88)90078-4CrossRefGoogle Scholar
Bai, Z. and Yin, Y. (1993). Limit of the smallest eigenvalue of a large dimensional sample covariance matrix. Ann. Prob. 21, 1275–1294.10.1214/aop/1176989118CrossRefGoogle Scholar
Chen, Z. and Dongarra, J. (2005). Condition numbers of Gaussian random matrices. SIAM J. Matrix Anal. Appl. 27, 603–620.10.1137/040616413CrossRefGoogle Scholar
Dembo, A. and Zeitouni, O. (2010). Large Deviations Techniques and Applications, corrected reprint of 2nd ed. Springer, Berlin.Google Scholar
Edelman, A. (1988). Eigenvalues and condition numbers of random matrices. SIAM J. Matrix Anal. Appl. 9, 543–560.10.1137/0609045CrossRefGoogle Scholar
Edelman, A. and Sutton, B. (2005). Tails of condition number distributions. SIAM J. Matrix Anal. Appl. 27, 547–560.10.1137/040614256CrossRefGoogle Scholar
Fey, A., van der Hofstad, R. and Klok, M. (2008). Large deviations for eigenvalues of sample covariance matrices, with applications to mobile communication systems. Adv. Appl. Prob. 40, 1048–1071.10.1239/aap/1231340164CrossRefGoogle Scholar
Gustafson, K. (2012). Antieigenvalue Analysis, World Scientific, Hackensack, NJ.10.1142/8247CrossRefGoogle Scholar
James, A. (1964). Distributions of matrix variates and latent roots derived from normal samples. Ann. Math. Statist. 35, 475–501.10.1214/aoms/1177703550CrossRefGoogle Scholar
Jiang, T. and Li, D. (2015). Approximation of rectangular beta-Laguerre ensembles and large deviations. J. Theoret. Prob. 28, 804–847.10.1007/s10959-013-0519-7CrossRefGoogle Scholar
Kevei, P. (2010). A note on asymptotics of linear combinations of iid random variables. Period. Math. Hungar. 60, 25–36.10.1007/s10998-010-1025-7CrossRefGoogle Scholar
Litvak, A., Pajor, A., Rudelson, M. and Tomczak-Jaegermann, N. (2005). Smallest singular value of random matrices and geometry of random polytopes. Adv. Math. 195, 491–523.10.1016/j.aim.2004.08.004CrossRefGoogle Scholar
Litvak, A., Tikhomirov, K. and Tomczak-Jaegermann, N. (2019). Small ball probability for the condition number of random matrices. In Geometric Aspects of Functional Analysis, ed. Klartag, B. and Milman, E., Vol. II, Springer, Berlin.Google Scholar
Muirhead, R. (1982). Aspects of Multivariate Statistical Theory. John Wiley, New York.10.1002/9780470316559CrossRefGoogle Scholar
Rogers, C. (1963). Covering a sphere with spheres. Mathematika 10, 157–164.10.1112/S0025579300004083CrossRefGoogle Scholar
Rudelson, M. (2008). Invertibility of random matrices: norm of the inverse. Ann. Math. 168, 575–600.10.4007/annals.2008.168.575CrossRefGoogle Scholar
Rudelson, M. and Vershynin, R. (2008). The Littlewood–Offord problem and invertibility of random matrices. Adv. Math. 218, 600–633.10.1016/j.aim.2008.01.010CrossRefGoogle Scholar
Rudelson, M. and Vershynin, R. (2009). Smallest singular value of a random rectangular matrix. Comm. Pure Appl. Math. 62, 1707–1739.10.1002/cpa.20294CrossRefGoogle Scholar
Srivastava, M. S. and Khatri, C. (1979). An Introduction to Multivariate Statistics. North-Holland, Amsterdam.Google Scholar
Tao, T. and Vu, V. (2009). Inverse Littlewood–Offord theorems and the condition number of random discrete matrices. Ann. Math. 169, 595–632.10.4007/annals.2009.169.595CrossRefGoogle Scholar
Tao, T. and Vu, V. (2010). Random matrices: the distribution of the smallest singular values. Geom. Funct. Anal. 20, 260–297.10.1007/s00039-010-0057-8CrossRefGoogle Scholar
Trefethen, L. and Bau, D. (1997). Numerical Linear Algebra. SIAM, Philadelphia, PA.10.1137/1.9780898719574CrossRefGoogle Scholar
Vershynin, R. (2012). Introduction to the Non-Asymptotic Analysis of Random Matrices. Cambridge University Press.10.1017/CBO9780511794308.006CrossRefGoogle Scholar