Hostname: page-component-6bf8c574d5-2jptb Total loading time: 0 Render date: 2025-02-22T18:26:34.860Z Has data issue: false hasContentIssue false
  • English
  • Français

Large-deviation results for triangular arrays of semiexponential random variables

Part of: Limit theorems Stochastic processes

Published online by Cambridge University Press:  08 February 2022

Thierry Klein ,
Agnès Lagnoux Open the ORCID record for Agnès Lagnoux [Opens in a new window]  and
Pierre Petit
Thierry Klein*
Affiliation:
Institut de Mathématiques de Toulouse; ENAC
Agnès Lagnoux*
Affiliation:
Institut de Mathématiques de Toulouse; UT2J
Pierre Petit*
Affiliation:
Institut de Mathématiques de Toulouse; UT3
*
*Postal address: Institut de Mathématiques de Toulouse; UMR5219. Université de Toulouse; ENAC - Ecole Nationale de l’Aviation Civile, Université de Toulouse, France. Email: thierry.klein@math.univ-toulouse.fr
**Postal address: Institut de Mathématiques de Toulouse; UMR5219. Université de Toulouse; CNRS. UT2J, F-31058 Toulouse, France. Email: lagnoux@univ-tlse2.fr
***Postal address: Institut de Mathématiques de Toulouse; UMR5219. Université de Toulouse; CNRS. UT3, F-31062 Toulouse, France. Email: pierre.petit@math.univ-toulouse.fr
Get access Rights & Permissions [Opens in a new window]

Abstract

Asymptotics deviation probabilities of the sum $S_n=X_1+\dots+X_n$ of independent and identically distributed real-valued random variables have been extensively investigated, in particular when 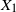$X_1$ is not exponentially integrable. For instance, Nagaev (1969a, 1969b) formulated exact asymptotics results for 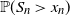$\mathbb{P}(S_n>x_n)$ with 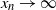$x_n\to \infty$ when 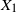$X_1$ has a semiexponential distribution. In the same setting, Brosset et al. (2020) derived deviation results at logarithmic scale with shorter proofs relying on classical tools of large-deviation theory and making the rate function at the transition explicit. In this paper we exhibit the same asymptotic behavior for triangular arrays of semiexponentially distributed random variables.

Keywords

Large deviationstriangular arraysemiexponential distributionWeibull-like distributionGärtner–Ellis theoremContraction principletruncated random variable

MSC classification

Primary: 60F10: Large deviations
Secondary: 60G50: Sums of independent random variables; random walks
Type
Original Article
Information
Journal of Applied Probability , Volume 59 , Issue 2 , June 2022 , pp. 399 - 420
Check for updates
Copyright
© The Author(s), 2022. Published by Cambridge University Press on behalf of Applied Probability Trust

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Billingsley, P. (2013). Convergence of Probability Measures. John Wiley, Chichester.Google Scholar
Borovkov, A. A. (2000). Large deviation probabilities for random walks with semiexponential distributions. Siberian Math. J. 41, 1290–1324.CrossRefGoogle Scholar
Borovkov, A. A. and Borovkov, K. A. (2008). Asymptotic Analysis of Random Walks (Encyc. Math. Appl. 118). Cambridge University Press.Google Scholar
Brosset, F., Klein, T., Lagnoux, T. and Petit, P. Large deviations at the transition for sums of Weibull-like random variables. To appear in Séminaire de Probabilités.Google Scholar
Cramér, H. (1938). Sur un nouveau théorème-limite de la théorie des probabilités. Actualités Sci. Ind. 736, 5–23.Google Scholar
Dembo, A. and Zeitouni, O. (1998). Large Deviations Techniques and Applications (Appl. Math. 38), 2nd ed. Springer, New York.CrossRefGoogle Scholar
Denisov, D., Dieker, A. B. and Shneer, V. (2008). Large deviations for random walks under subexponentiality: The big-jump domain. Ann. Prob. 36, 1946–1991.CrossRefGoogle Scholar
Feller, W. (1943). Generalization of a probability limit theorem of Cramér. Trans. Amer. Math. Soc. 54, 361–372.Google Scholar
Gut, A. (1992). Complete convergence for arrays. Periodica Mathematica Hungarica 25, 51–75.CrossRefGoogle Scholar
Gut, A. (1992). The weak law of large numbers for arrays. Statist. Prob. Lett. 14, 49–52.CrossRefGoogle Scholar
Hu, T.-C., Moricz, F. and Taylor, R. (1989). Strong laws of large numbers for arrays of rowwise independent random variables. Acta Math. Hungarica 54, 153–162.CrossRefGoogle Scholar
Janson, S. (2001). Asymptotic distribution for the cost of linear probing hashing. Random Structures Algorithms 19, 438–471.CrossRefGoogle Scholar
Kinchin, A. (1929). Über einer neuen Grenzwertsatz der Wahrscheinlichkeitsrechnung. Math. Ann. 101, 745–752.Google Scholar
Klein, T., Lagnoux, A. and Petit, P. (2021). Deviation results for sparse tables in hashing with linear probing. Preprint, arXiv:1603.02235.Google Scholar
Linnik, J. V. (1961). On the probability of large deviations for the sums of independent variables. In Proc. 4th Berkeley Symp. Math. Statist. Prob., Vol. II. University of California Press, Berkeley, CA, pp. 289–306.Google Scholar
Mikosch, T. and Nagaev, A. V. (1998). Large deviations of heavy-tailed sums with applications in insurance. Extremes 1, 81–110.CrossRefGoogle Scholar
Nagaev, A. V. (1969). Integral limit theorems taking large deviations into account when Cramér’s condition does not hold. I. Theory Prob. Appl. 14, 51–64.CrossRefGoogle Scholar
Nagaev, A. V. (1969). Integral limit theorems taking large deviations into account when Cramér’s condition does not hold. II. Theory Prob. Appl. 14, 193–208.CrossRefGoogle Scholar
Nagaev, A. V. (1979). Large deviations of sums of independent random variables. Ann. Prob. 7, 745–789.CrossRefGoogle Scholar
Petrov, V. V. (1954). Generalization of Cramér’s limit theorem. Uspehi Matem. Nauk (N.S.) 9, 195–202.Google Scholar
Petrov, V. V. and Robinson, J. (2008). Large deviations for sums of independent non-identically distributed random variables. Commun. Statist. Theory Meth. 37, 2984–2990.CrossRefGoogle Scholar
Plachky, D. and Steinebach, J. (1975). A theorem about probabilities of large deviations with an application to queuing theory. Period. Math. Hungar. 6, 343–345.CrossRefGoogle Scholar
Smirnov, N. V. (1933). On the probabilities of large deviations. Mat. Sb. 40, 443–454.Google Scholar