Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Zhang, Hui Zeng
Zhao, Min Zhi
and
Wang, Lei
2013.
On first returning time and last exit time of a class of Markov chain.
Acta Mathematica Sinica, English Series,
Vol. 29,
Issue. 2,
p.
331.

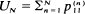 plays an important role. (See for example, Orey (1971), Athreya and Ney (1980).) In this paper we consider the rate of growth of
plays an important role. (See for example, Orey (1971), Athreya and Ney (1980).) In this paper we consider the rate of growth of 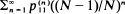 as
as 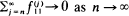 as
as 