Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2024-12-28T19:18:51.701Z Has data issue: false hasContentIssue false
  • English
  • Français

The limit distribution for maxima of ‘weighted' rth-nearest-neighbour distances

Published online by Cambridge University Press:  14 July 2016

Norbert Henze
Norbert Henze*
Affiliation:
University of Hannover
*
∗ Postal address: Lehrgebiet Mathematische Stochastik, Universität Hannover, Welfengarten 1, D-3000 Hannover 1, W. Germany.
Get access Rights & Permissions [Opens in a new window]

Abstract

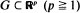Let X1, X2, · ··, Xn be independent identically distributed random points with common density f(x), taking values in a bounded region (p ≧ 1). We obtain the limit distribution, as n → ∞, for the maximum value of the suitably ‘weighted' (according to f(x)) rth-nearest-neighbour distances of Χ1, · ··, Χ n (r ≧ 1 fixed) provided that f(x) is bounded from below by a positive constant and a weak continuity condition holds. This is achieved by refining an argument used by the author (Henze (1981)) to derive the limit distribution in the special case r = 1. Edge-effects are eliminated by defining, for each Xi, the distance to the boundary of G to be the ‘rth-nearest-neighbour distance' if it is smaller than the distance to the rth nearest neighbour among the remaining points. Applications to a multivariate test of goodness of fit are given.

Keywords

MAXIMA OF rth-NEAREST-NEIGHBOUR DISTANCESMULTIVARIATE TEST OF GOODNESS OF FITEXTREME-VALUE DISTRIBUTION
Type
Research Papers
Information
Journal of Applied Probability , Volume 19 , Issue 2 , June 1982 , pp. 344 - 354
Copyright
Copyright © Applied Probability Trust 1982 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Galambos, J. (1978) The Asymptotic Theory of Extreme Order Statistics. Wiley, New York.Google Scholar
Henze, N. (1981) Ein asymptotischer Satz über den maximalen Minimalabstand von unabhängigen Zufallsvektoren mit Anwendung auf einen Anpassungstest im ℝ p und auf der Kugel. Doctoral dissertation, University of Hannover.Google Scholar
Weiss, L. (1960) A test of fit based on the largest sample spacing. J. SIAM 8, 295–299.Google Scholar