Hostname: page-component-cd9895bd7-7cvxr Total loading time: 0 Render date: 2024-12-28T15:50:15.620Z Has data issue: false hasContentIssue false
  • English
  • Français

A limit theorem for point processes by applications

Published online by Cambridge University Press:  14 July 2016

Prem S. Puri
Prem S. Puri*
Affiliation:
Purdue University
Get access Rights & Permissions [Opens in a new window]

Abstract

Let 0 ≦ T1 ≦ T2 ≦ ·· · represent the epochs in time of occurrences of events of a point process N(t) with N(t) = sup{k : Tk ≦ t}, t ≧ 0. Besides certain mild conditions on the process N(t) (see Conditions (A1)– (A3) in the text) we assume that for every k ≧ 1, as t →∞, the vector (t – TN(t), t – TN(t)–1, · ··, t – TN(t)–k+1) converges in law to a k-dimensional distribution which coincides with that of a random vector ξ k = (ξ1, · ··, ξ k) necessarily satisfying P(0 ≦ ξ1 ≦ ξ2 ≦ ·· ·≦ ξk) = 1. Let R(t) be an arbitrary function defined for t ≧ 0, satisfying 0 ≦ R(t) ≦ 1, ∀0 ≦ t <∞, and certain mild conditions (see Conditions (B1)– (B4) in the text). Then among other results, it is shown that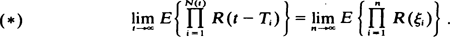

The paper also deals with conditions under which the limit (∗) will be positive. The results are applied to several point processes and to the situations where the role of R(t) is taken over by an appropriate transform such as a probability generating function, where conditions are given under which the limit (∗) itself will be a transform of an honest distribution. Finally the results are applied to the study of certain characteristics of the GI/G/∞ queue apparently not studied before.

Keywords

POINT PROCESSESLIMIT THEOREMSRENEWAL PROCESSESNON-HOMOGENEOUS POISSON PROCESSESGI/G/∞QUEUEPROCESSES WITH IMMIGRATIONBRANCHING PROCESSES
Type
Research Papers
Information
Journal of Applied Probability , Volume 15 , Issue 4 , December 1978 , pp. 726 - 747
Copyright
Copyright © Applied Probability Trust 1978 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1] Feller, W. (1971) An Introduction to Probability Theory and its Applications , Vol. 2, 2nd edn. Wiley, New York.Google Scholar
[2] Harris, T. E. (1963) The Theory of Branching Processes. Springer-Verlag, Berlin.CrossRefGoogle Scholar
[3] Heathcote, C. R. (1965) A branching process allowing immigration. J. R. Statist. Soc. B27, 138–143.Google Scholar
[4] Heathcote, C. R. (1966) Corrections and comments on the paper, ‘A branching process allowing immigration.’ J. R. Statist. Soc. B28, 213–217.Google Scholar
[5] Jagers, P. (1968) Age-dependent branching processes allowing immigration. Theory Prob. Appl. 13, 225–236.Google Scholar
[6] Kaplan, N. (1973) The multitype Galton-Watson process with immigration. Ann. Prob. 1, 947–953.Google Scholar
[7] Kaplan, N. (1974) The supercritical p-dimensional Galton-Watson process with immigration. Math. Biosci. 22, 1–18.CrossRefGoogle Scholar
[8] Kaplan, N. (1974) Multidimensional age-dependent branching processes allowing immigration: the limiting distribution. J. Appl. Prob. 11, 225–236.Google Scholar
[9] Kaplan, N. (1975) Limit theorems for a GI/G/8 queue. Ann. Prob. 3, 780–789.Google Scholar
[10] Kaplan, N. and Pakes, A. G. (1974) Supercritical age-dependent branching processes with immigration. Stoch. Proc. Appl. 2, 371–389.CrossRefGoogle Scholar
[11] Pakes, A. G. (1972) Limit theorems for an age-dependent branching process with immigration. Math. Biosci. 14, 221–234.Google Scholar
[12] Pakes, A. G. (1974) On supercritical Galton-Watson processes allowing immigration. J. Appl. Prob. 11, 814–817.Google Scholar
[13] Pakes, A. G. (1975) Some results for nonsupercritical Galton-Watson processes with immigration. Math. Biosci. 24, 71–92.CrossRefGoogle Scholar
[14] Pakes, A. G. (1975) On Markov branching processes with immigration. Sankhya A37, 129–138.Google Scholar
[15] Pakes, A. G. and Kaplan, N. (1974) On the subcritical Bellman–Harris process with immigration. J. Appl. Prob. 11, 652–668.Google Scholar
[16] Pakes, A. G. and Parthasarathy, P. R. (1975) Some convergence rate results for the Bellman–Harris process with immigration. Math. Biosci. 26, 207–216.Google Scholar
[17] Puri, P. S. (1967) Some limit theorems on branching processes related to development of biological populations. Math. Biosci. 1, 77–94.Google Scholar
[18] Sevast'yanov, B. A. (1957) Limit theorems for branching processes of special form. Theory Prob. Appl. 2, 321–331.Google Scholar
[19] Yang, Y. S. (1972) On branching processes allowing immigration. J. Appl. Prob. 9, 24–31.Google Scholar