Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Watson, G.S.
1983.
Studies in Econometrics, Time Series, and Multivariate Statistics.
p.
559.
Vitale, Richard A.
1985.
The steiner point in infinite dimensions.
Israel Journal of Mathematics,
Vol. 52,
Issue. 3,
p.
245.
Runnenburg, J.Th.
1985.
PROBABILITY THEORY AND ITS APPLICATIONS.
Statistica Neerlandica,
Vol. 39,
Issue. 2,
p.
181.
Watson, G. S.
1988.
The Langevin distribution on high dimensional spheres.
Journal of Applied Statistics,
Vol. 15,
Issue. 2,
p.
123.
Holmes, R. B.
1991.
On Random Correlation Matrices.
SIAM Journal on Matrix Analysis and Applications,
Vol. 12,
Issue. 2,
p.
239.
Kenney, C. S.
and
Laub, A. J.
1994.
Small-Sample Statistical Condition Estimates for General Matrix Functions.
SIAM Journal on Scientific Computing,
Vol. 15,
Issue. 1,
p.
36.
Gudmundsson, T.
Kenney, C. S.
and
Laub, A. J.
1995.
Small-Sample Statistical Estimates for Matrix Norms.
SIAM Journal on Matrix Analysis and Applications,
Vol. 16,
Issue. 3,
p.
776.
1999.
Directional Statistics.
p.
395.
Dryden, Ian L.
2005.
Statistical analysis on high-dimensional spheres and shape spaces.
The Annals of Statistics,
Vol. 33,
Issue. 4,
Хохлов, Владимир Иванович
and
Khokhlov, Vladimir Ivanovich
2005.
Свойства проекций распределения, равномерного на сфере в $R^s$. I.
Теория вероятностей и ее применения,
Vol. 50,
Issue. 3,
p.
501.
Jiang, Tiefeng
2006.
How many entries of a typical orthogonal matrix can be approximated by independent normals?.
The Annals of Probability,
Vol. 34,
Issue. 4,
Khokhlov, V. I.
2006.
The Uniform Distribution on a Sphere in ${\bf R}^S$. Properties of Projections. I.
Theory of Probability & Its Applications,
Vol. 50,
Issue. 3,
p.
386.
López-Ruiz, Ricardo
and
Calbet, Xavier
2007.
Derivation of the Maxwellian distribution from the microcanonical ensemble.
American Journal of Physics,
Vol. 75,
Issue. 8,
p.
752.
Spruill, Marcus
2007.
Asymptotic Distribution of Coordinates on High Dimensional Spheres.
Electronic Communications in Probability,
Vol. 12,
Issue. none,
Calbet, Xavier
and
López-Ruiz, Ricardo
2007.
Extremum complexity distribution of a monodimensional ideal gas out of equilibrium.
Physica A: Statistical Mechanics and its Applications,
Vol. 382,
Issue. 2,
p.
523.
Jiang, Tiefeng
2010.
The Entries of Haar-Invariant Matrices from the Classical Compact Groups.
Journal of Theoretical Probability,
Vol. 23,
Issue. 4,
p.
1227.
Grafarend, Erik W.
and
Awange, Joseph L.
2012.
Linear and Nonlinear Models.
p.
461.
Grafarend, Erik W.
and
Awange, Joseph L.
2012.
Linear and Nonlinear Models.
p.
383.
Grafarend, Erik W.
and
Awange, Joseph L.
2012.
Linear and Nonlinear Models.
p.
477.
Grafarend, Erik W.
and
Awange, Joseph L.
2012.
Linear and Nonlinear Models.
p.
183.

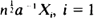 , ···,
, ···, 